机器学习

考试

  • 选择
  • 判断
  • 简答
  • 简答
  • 综合

Introduction

什么是机器学习？

“Machine Learning is fields of study that gives computers the ability to learn without being explicitly programmed.”

机器学习是这样的领域，它赋予计算机 学习的能力，（这种学习能力）不是通 过显著式编程获得的。

非显著式编程

– 让计算机自己总结规律的编程方法

– 通过数据、经验自动地学习，完成给定任务

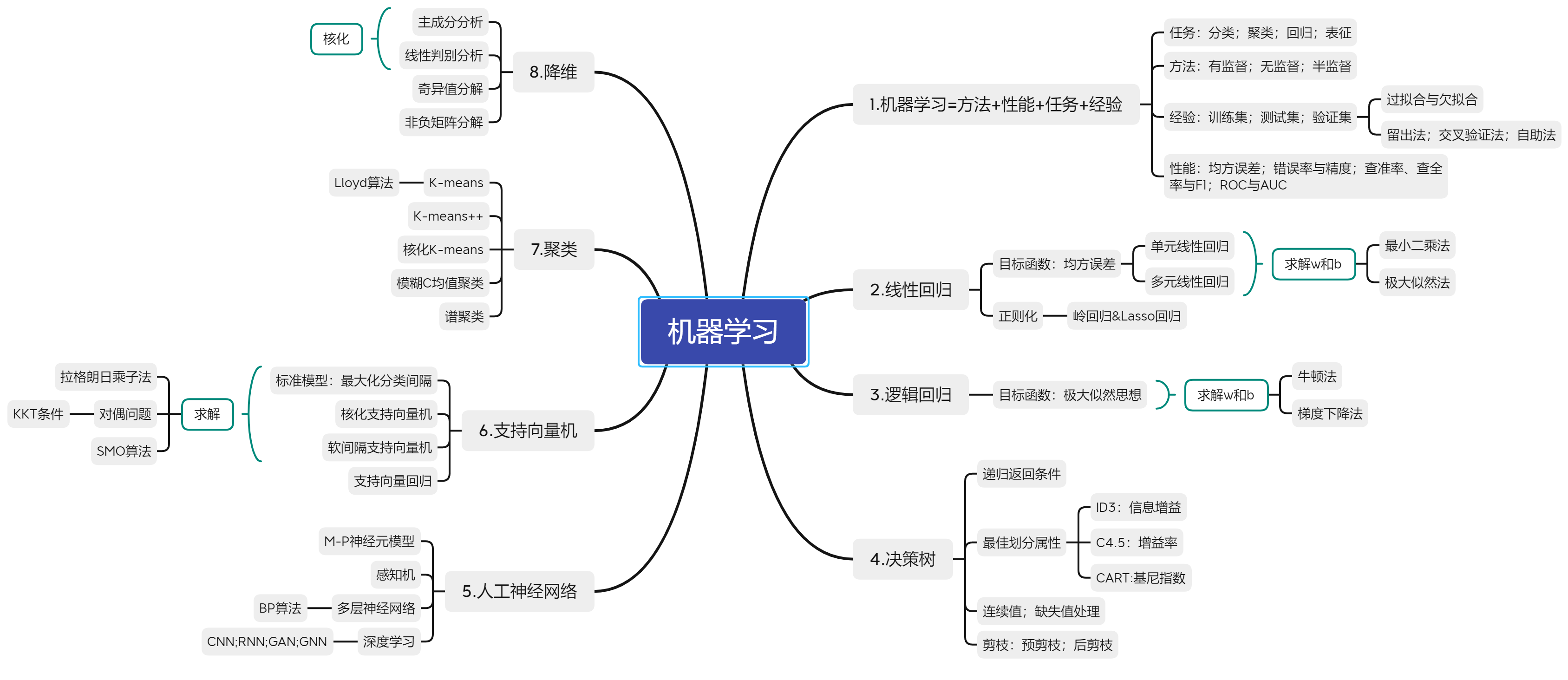
机器学习=方法+性能+任务+经验

• 方法-A: 各种机器学习方法
• 任务-T：机器学习要解决的问题
• 性能-P：方法针对任务的性能评估准则
• 经验-E：训练模型的数据，实例

对于T，A的选择相对灵活，也是机器学习课程主要学习 的内容，P是评价A在解决T的性能指标，E是机器学习动 力与源泉。

一个计算机程序被称为可以学习，是指它能够针对某个T 和某个P，从E中学习。这种学习的特点是，它在T上的被 P所衡量的性能，会随着E的增加而提高。

T：编写计算机程序识别菊花和玫瑰

– A：某种机器学习算法

– P：识别的正确率（识别率）

– E：一大堆菊花和玫瑰的图片（训练样本）

T：人脸识别

– A：线性回归

– P：人脸识别准确率

– E：已标定身份的人脸图片数据

T：象棋博弈

– A: 人工神经网络

– P: 对随机对手的获胜比率

– E: 指令化棋谱

T：股价预测

– A: 多项式回归

– P: 估价误差（方差）

– E: 不同股票近三年各交易日股价数据

Fundamental Task

机器学习基本任务：

  • 离散值

    • 分类（Classification）

      • 分类（图像、视频、文本………）
      • 识别（语音、人脸、指纹…….）
      • 检测（行人、车辆、军事目标…….）

    • 聚类（Clustering）

      • 分割（图像、视频）、背景建模
      • 数据挖掘
      • 字典学习（视觉信息，文本）

  • 连续值

    • 回归（Regression）
      • 年龄估计
      • 形状分析、表情分析、运动分析等
    • 表征（Representation）
      • 特征提取（便于前三个任务解决）
      • 数据重构, 图像处理
      • 信息检索

Experience

经验E是由人工采集并输入计算机

经验E是由计算机与环境互动产生

Approaches

方法分类（根据学习形式）

  • 有监督学习（Supervised Learning）
    • 数据都有明确的标签，根据机器学习产生的模型 可以将新数据分到一个明确的类或得到一个预测 值。
    • 支持向量机、贝叶斯分类器、决策树、线性判别分析…….
  • 无监督学习（Unsupervised Learning）
    • 数据没有标签，机器学习出的模型是从数据中提取出来的模式（提取决定性特征或者聚类等）
    • K均值、Meanshift、主成分分析、典型相关分析 ……
  • 半监督学习（Semi-supervised Learning）
    • 部分数据有明确的标签，根据机器学习产生的模 型可以将新数据分到一个明确的类或得到一个预 测值。
    • 图直推学习、超图直推学习……

无监督学习

需要假设：

  1. 同一类的训练数据在空间中距离更近
  2. 利用样本空间信息
  3. 设计算法将他们聚集为两类
  4. 实现无监督学习

性能度量与评估

The Performance measure and evaluation of machine learning approaches

Experiences（经验）

Experience = The data we have for training the machine learning model.

对于特定机器学习任务，已存在的可利 用数据即是解决该机器学习任务的经验。

数据为王：大数据=丰富经验=训练更好的机器学习模型

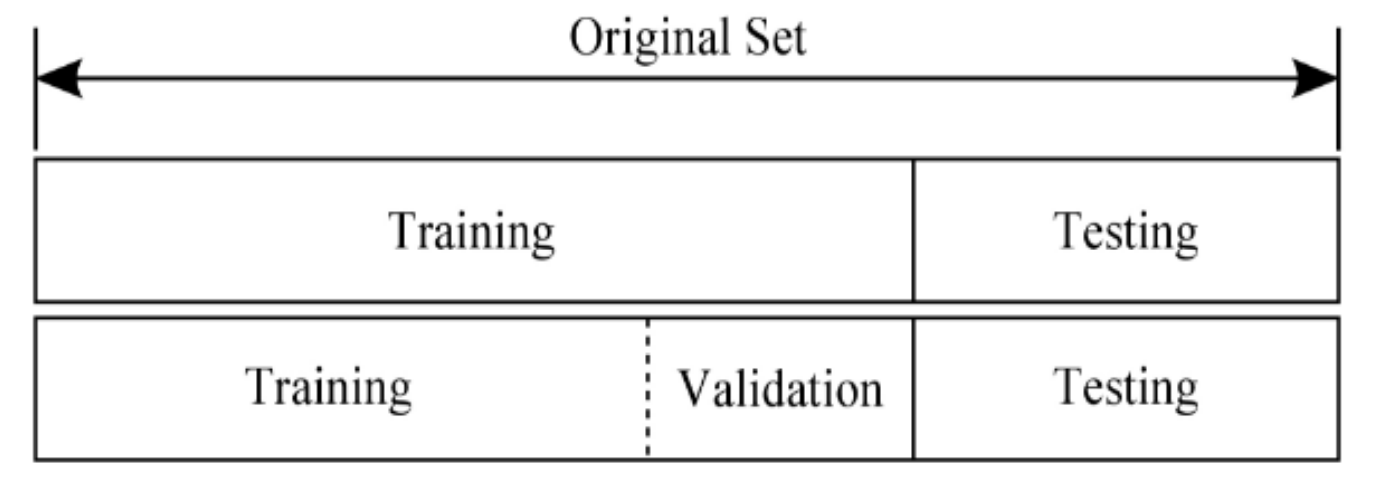
数据划分

  • 训练集（Training Set）
    • 用来训练模型或确定模型参数。
  • 测试集（Testing Set）
    • 测试已经训练好的模型的推广能力。
  • 验证集（Validation set）可选
    • 用来做模型选择（model selection），即做模型的最 终优化及确定的。

误差与精度

  • 误差（error）：学习器（Learner）的实际预测输出与样本的真实输出之间的差异。
  • 错误率（error rate）: 被错误分类的样本在总样本中的比例。
  • 精度（accuracy）:被正确分类的样本在总样本中的比例，即1−errorrate1-error rate。
  • 训练误差（training error）:学习器在训练集上的误差。
  • 经验误差（empirical error）:即训练误差
  • 泛化误差（generalization error): 在新样本的误差，实际误差！
  • 测试误差（Testing Error） :学习器在测试集上的误差，用来近似泛化误差。

希望得到泛化误差小的学习器，然而，我们事先并不知 道新样本什么样，实际能做的是努力使经验误差最小化。

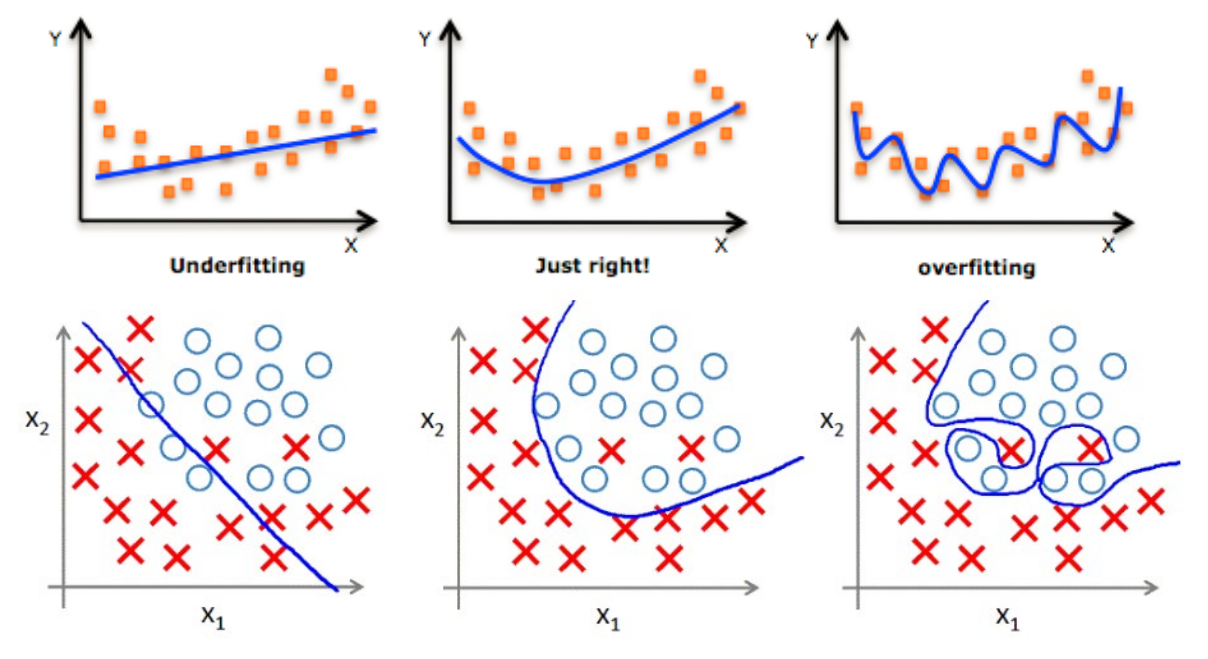
过拟合和欠拟合

过拟合(Overfitting): 为了得到一致假设而使假设变得过度严格。

欠拟合(Underfitting): 模型没有很好地捕捉到数据特征，不能够很好地拟合数据

数据集划分策略

利用测试集或验证集评估学习器的泛化误差，进而进行模型优化与选择，避免过拟合。

常见的划分策略

  • 留出法
    • 直接将数据集D划分为两个互斥集合
    • 测试\训练集划分尽量保持数据分布一致性
    • 采用合理的采样，合理地控制训练集与测试 集的比例。
    • 多次使用留出法，重复进行实验评估并求均 值，减少数据分布差异造成的偏差。
  • 交叉验证法
    • 把数据集等 分为n份相互不重叠的子集，每次以其中1份子集作为 测试集，其余n-1份子集作为训练集，重复n次，直至 所有子集都作为测试集进行过一次实验评估，最后返 回n次实验评估的平均结果。
    • 交叉验证是最常见数据集划分方法。
    • 留一法（Leave-One-Out，简称LOO）：特殊的交叉验 证法，每个被划分的子集只有一个样本。
      • 优点： • 训练集比例高，训练出来模型与用所有数据进行训练的模 型相似度高。
      • 缺点： • 评估开销大 • 测试集比例太低，模型调参不便。
  • 自助法
    • 假设一个由m个样本组成数据集D，对其进行m次随机采样构造一个由m个样本组成 新数据集D’, 由于m次随机采样可能会对D中部分样本 重复采样，所以D’中有部分样本是完全相同，而D中 有部分样本是没有被采样到数据集D’中。因此我们可 以把D中这部分没有被采样到样本D\D’构造测试集， 而D’作为训练集。
    • 这种没被采样到样本在数据集D中比例一般占 25%~36.8%之间。
    • 自助法通常用于数据集较小或难以有效划分训练/测试集情况。

数据集划分各子集之间不能有重合

没有免费午餐定理

– 无论学习算法𝔏a多聪明、学习算法𝔏𝑏𝑏 多笨拙，它们 的期望性能竟然相同！

– 任何一个预测函数，如果在一些训练样本上表现好 ，那么必然在另一些训练样本上表现不好，如果不 对数据在特征空间的先验分布有一定假设，那么表 现好的与表现不好的情况一样多。

在设计机器学习算法时有一个假设： 在特征空间上距离接近的样本,他 们属于同一个类别的概率会更高

常见性能度量

– 均方误差

– 错误率与精度

– 查准率、查全率与F1

– ROC与AUC

均方误差（mean squared error）

  • 多用于度量学习器解决回归任务的性能

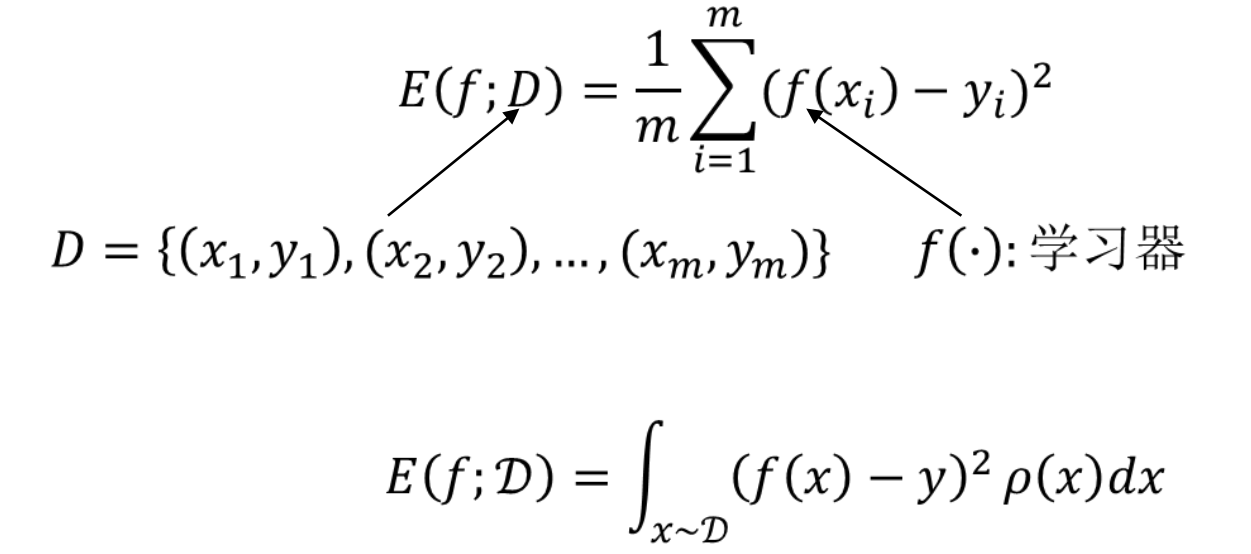
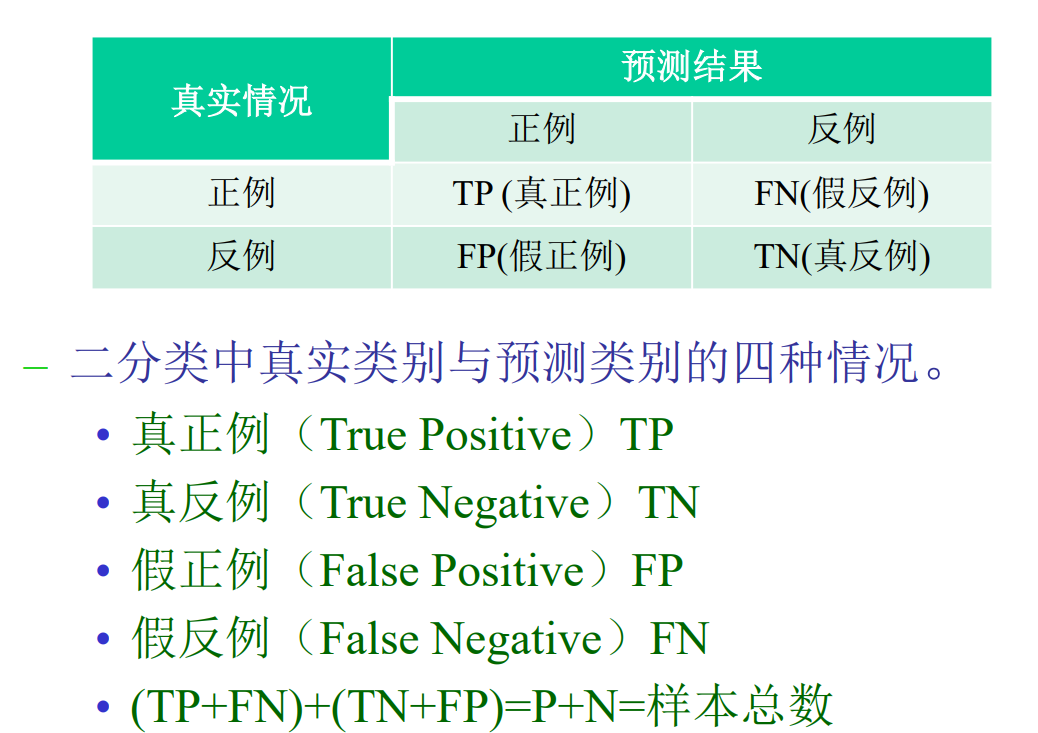
错误率与精度

  • 多用于评估分类任务的性能

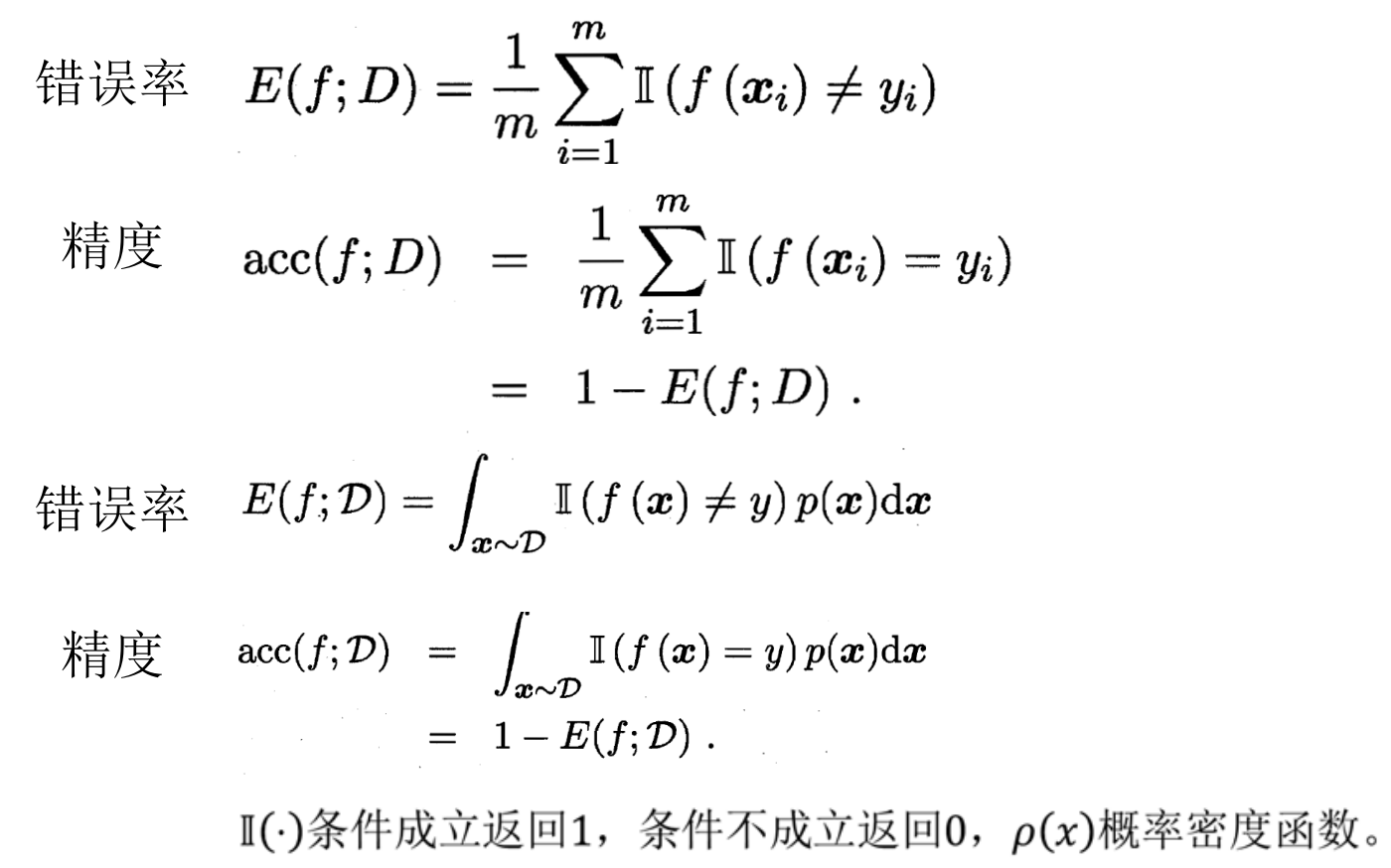
查准率、查全率、F1

  • 查准率(Precision)
    • 被正确分类的正例样本占所有被分类为正例样本的比例
    • P=TPTP+FPP=\frac{TP}{TP+FP}
  • 查全率(Recall)
    • 被正确分类的正例样本占所有正例样本的比例
    • R=TPTP+FNR=\frac{TP}{TP+FN}
    • 查全率与查准率是一对相互矛盾的度量

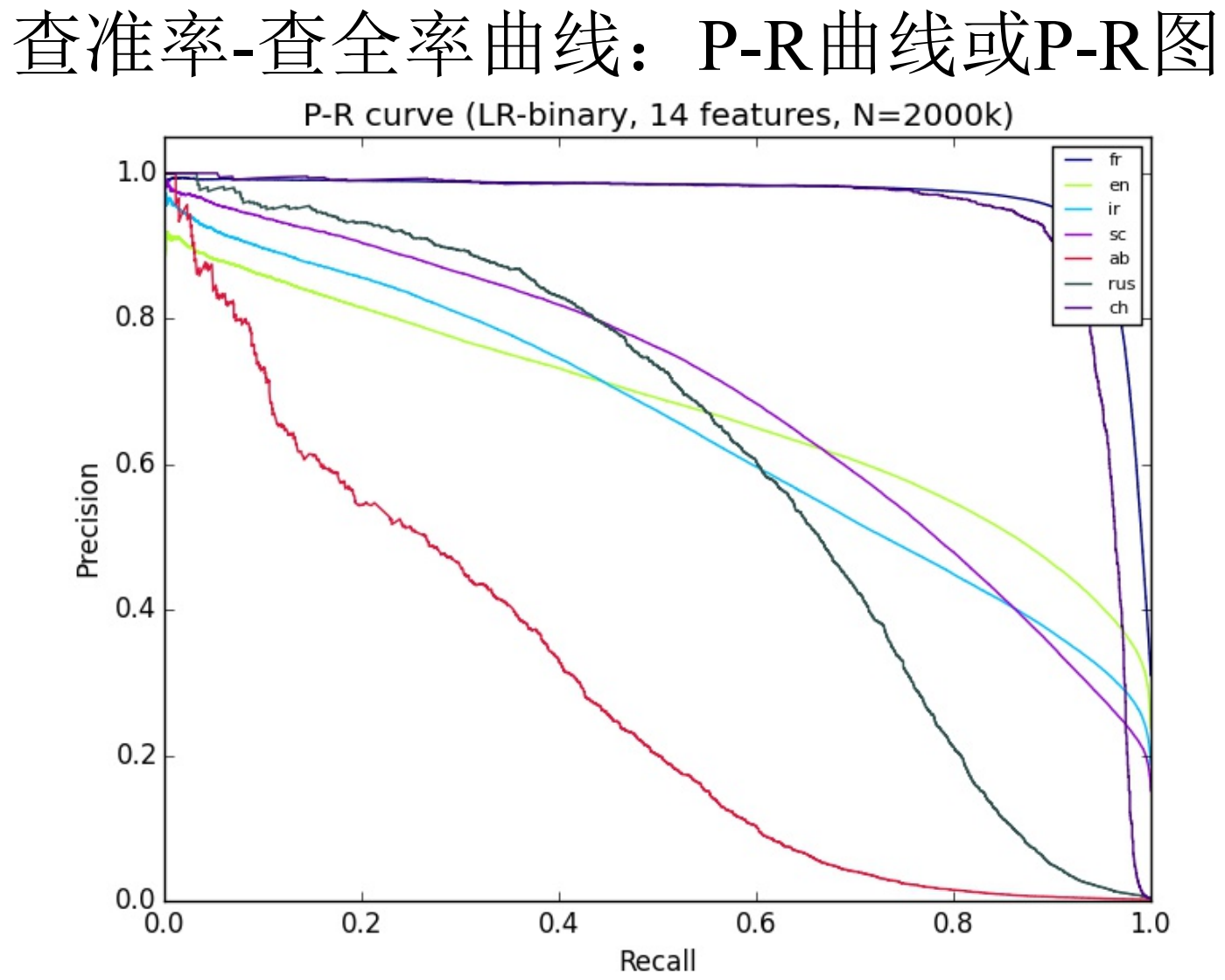
基于查准率-查全率的学习器性能度量：

平衡点（Break-Even Point, 简称BEP）

查准率等于查全率

F1−ScoreF_1-Score查准率和查全率的 调和平均

  • F1=2×P×RP+R=2×TP样本总数+TP−TNF_1=\frac{2\times{P}\times{R}}{P+R}=\frac{2\times{TP}}{样本总数+TP-TN}
  • 多用于评估检索与检测任务的性能

二分类问题的性能度量探讨：

根据置信度对样本进行降序排序，一个泛化性能较强的学 习器应该满足一下特征：

正例拥有高置信度，因此排序的 排列比较靠前，负例拥有置信度较低，排名应靠后。

受试者工作特征（Receiver Operating Characteristic, 简称ROC ）曲线：

真正例率（True Positive Rate, 简称TPR）—查全率

TPR=TPP=TPTP+FN\text{TPR}=\frac{\text{TP}}{P}=\frac{\text{TP}}{\text{TP}+\text{FN}}

假正例率（False Positive Rate,简称FPR）

FPR=FPN=FPTN+FPFPR=\frac{FP}{N}=\frac{FP}{TN+FP}

AUC

  • ROC曲线下的面积
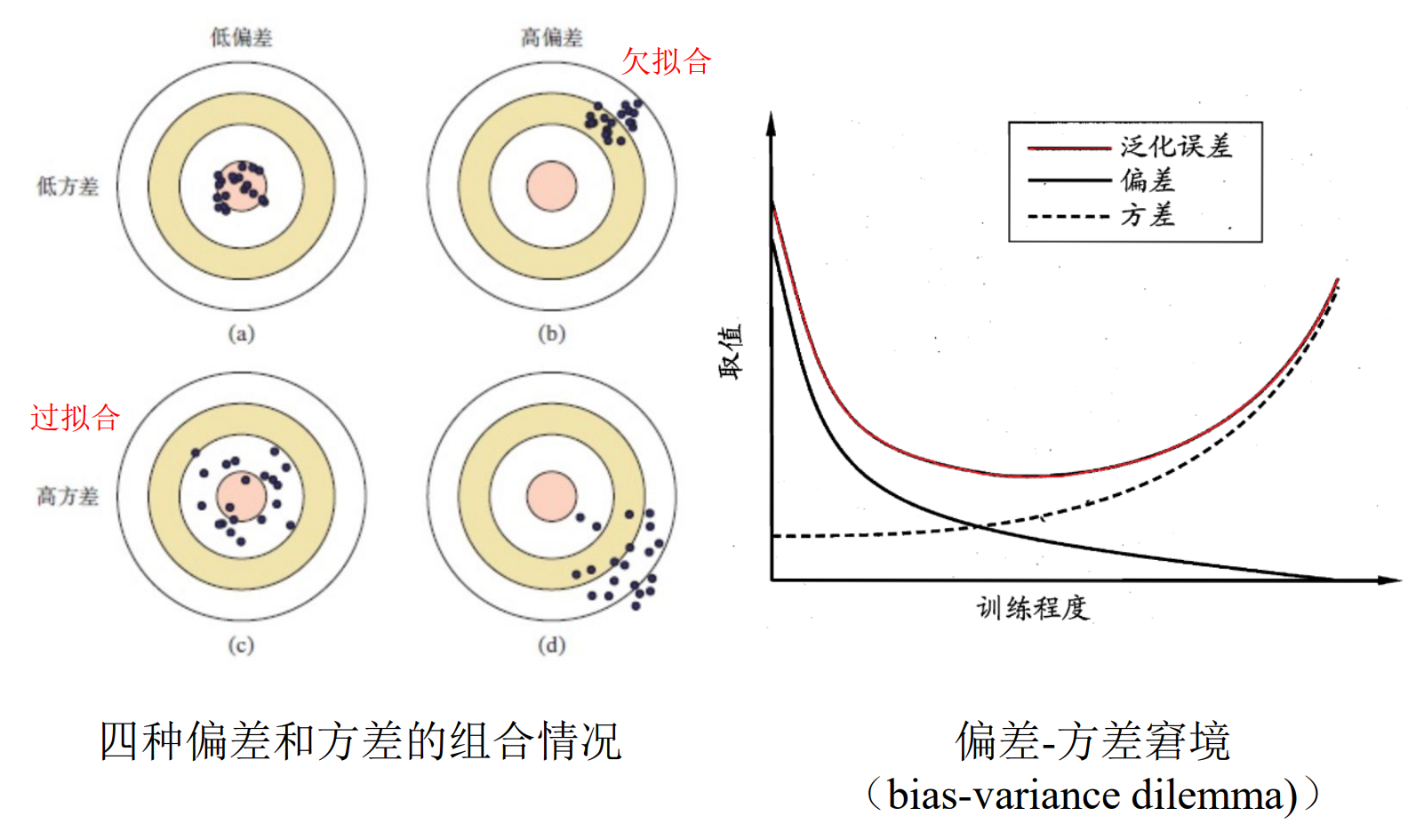
  • AUC=12∑i=1m-1(xi+1−xi)⋅(yi+yi+1)\text{AUC}=\frac{1}{2}\sum_{i=1}^{\text{m-1}}(x_{i+1}-x_i)\cdot(y_i+y_{i+1})

偏差与方差

E(f;D)=bias2(x)+var(x)+ε2\begin{aligned} \\ E(f;D)&& =bias^2\left(\boldsymbol{x}\right)+var\left(\boldsymbol{x}\right)+\varepsilon^2 \end{aligned}

  • 偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
  • 方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
  • 表达了在当前任务上任何学习算法所能达到的期 望泛化误差的下界，即刻画了学习问题本身的难度。

线性回归

监督学习（ Supervised Learning ）

回归与分类的区别

均是挖掘和学习输入变量和输出变量之间潜在关系模型，基于学习所得模型将输入变量映射到输出变量。

回归分析：学习得到一函数将输入变量映射到连续输出空间， 如价格和温度等，即值域是连续空间。

分类模型：学习得到一函数将输入变量映射到离散输出空间， 如人脸和汽车等，即值域是离散空间。

• 数据的相关性是普遍存在的。

• 回归是分析变量之间相关性的重要工具 – 碳排放量与气候变暖 – 商品广告投放量与商品销售量

• 回归分析：分析不同变量之间存在关系

• 回归模型：刻画不同变量之间关系的模型

• 如果这个模型是线性的——线性回归模型

image-20230616210135018

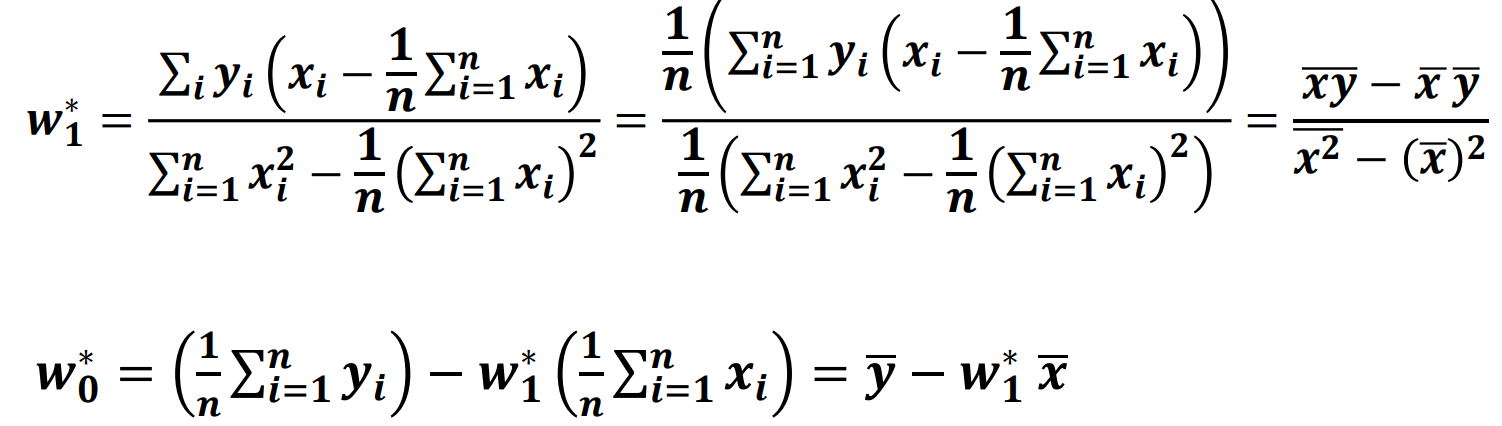
image-20230616210241748

岭回归&Lasso回归

image-20230616210915875

正则化模型

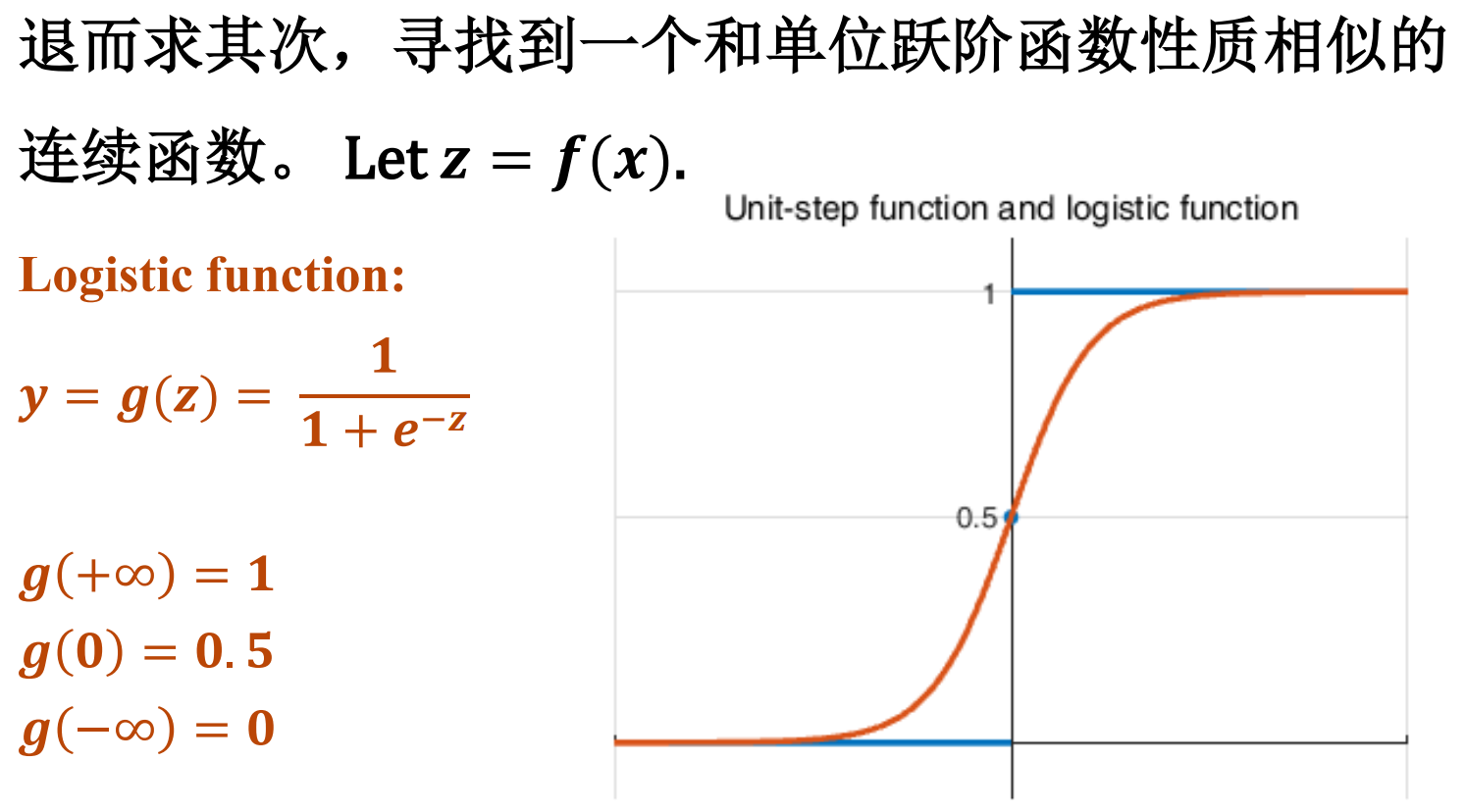
逻辑回归

image-20230616211717827

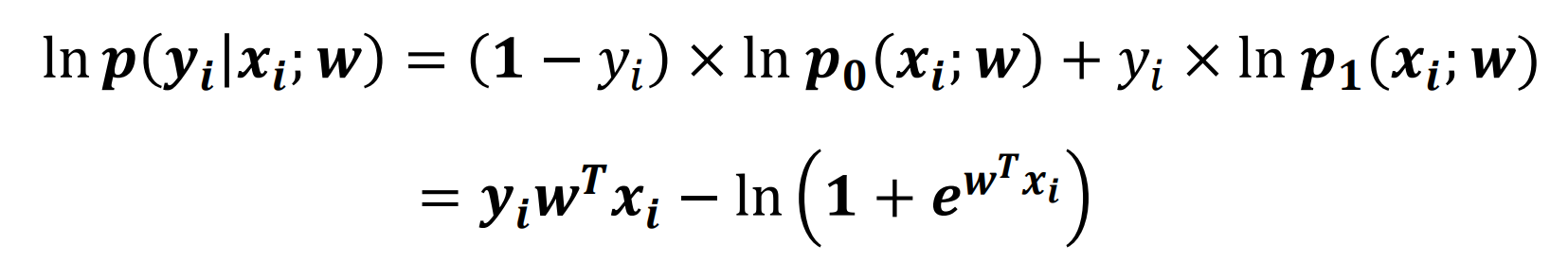
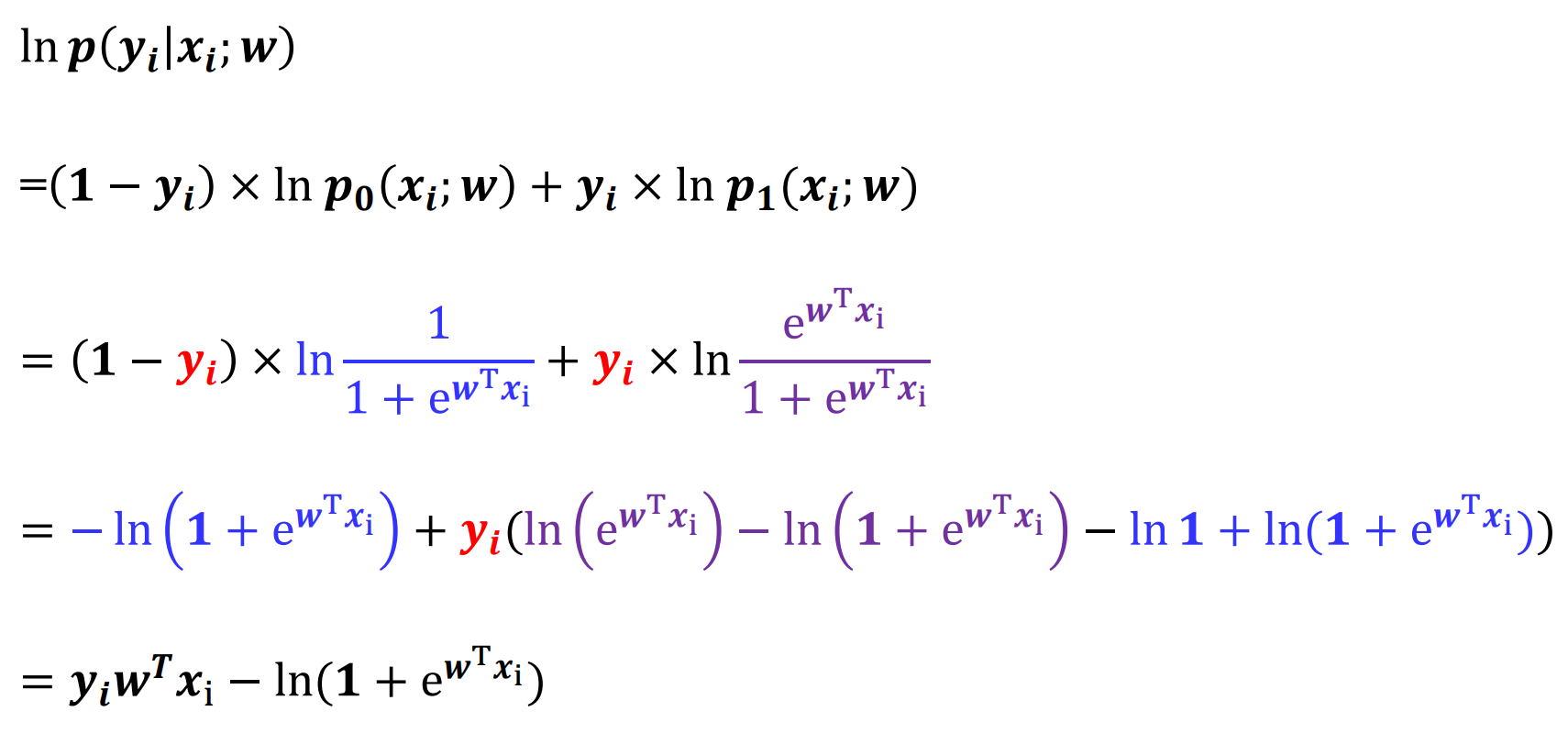
决策树

决策树（decision tree）：构建 一个基于属性的树形分类器。

  • 每个非叶结点表示一个特征属性上的测试（分割）
  • 每个分支代表这个特征属性在某 个值域上的输出
  • 每个叶结点存放一个类别

使用决策树进行决策的过程就是从根结点开始， 测试待分类项中相应的特征属性，并按照其值选 择输出分支，直到到达叶子结点，将叶子结点存 放的类别作为决策结果。

决策树构建：分治法思想（递归） – 对于当前结点返回递归条件：

① 当前结点样本均属于同一类别，无需划分。

② 当前属性集为空。

③ 所有样本在当前属性集上取值相同，无法划分。

④ 当前结点包含的样本集合为空，不能划分。

决策树的核心

  • 定义最佳划分属性：
    • 经过属性划分后，不同类样本被更好的分离。
    • 理想情况：划分后样本被完美分类。即每个分支的样本都属于同一类。
    • 实际情况：不可能完美划分！尽量使得每个分支某 一类样本比例尽量高！即尽量提高划分后子集的纯 度（purity）。
  • 最佳划分属性目标：
    • 提升划分后子集的纯度
    • 降低划分后子集的不纯度

ID3

纯度↑=确定性↑=信息量↓

度量信息量——信息熵:

Ent(D)=−∑k=1∣y∣pklog⁡2pkEnt(D)=-\sum_{k=1}^{|y|}p_k\log_2p_k

信息熵用来度量信息量，信息熵值越小，说明样本集的纯度越高。

利用划分后的信息增益来判断属性划分的优 劣性。

定义关于属性划分后信息熵度量：

16869832188321686983218564.png

信息增量准则对可取值数目较多的属性有所偏好。

C4.5

增益率（Gain Ratio）

Gain−ratio(D,a)=Gain(D,a)IV(a){Gain-ratio}(D,a)=\frac{Gain(D,a)}{IV(a)}

IV(𝑎)称为属性𝑎的“固有值”（Intrinsic Value）

IV(a)=−∑v=1V∣Dv∣∣D∣log⁡2∣Dv∣∣D∣IV(a)=-\sum_{v=1}^V\frac{|D^v|}{|D|}\log_2\frac{|D^v|}{|D|}

C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用一个启发式：

先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率高的属性。

CART

判断准则——基尼指数（Gini Index）：

Gini(Dν)=1−∑k=1∣y∣pk2Gini_index(D)=∑v=1∣V∣∣Dv∣∣D∣Gini(Dv)\begin{gathered} {Gini}(D^{\nu})=1-\sum_{k=1}^{|y|}p_k^2 \\ {Gini\_index}(D)=\sum_{v=1}^{|V|}\frac{|D^v|}{|D|}\text{Gini}(D^v) \end{gathered}

Gini(D)越小，则数据集D的纯度越高

总结

16869847058311686984705364.png

神经网络

神经网络是由具有适应性的简单单元组成的广泛并行互 连的网络，它的组织能够模拟生物神经系统对真实世界物体所 做的交互反应。

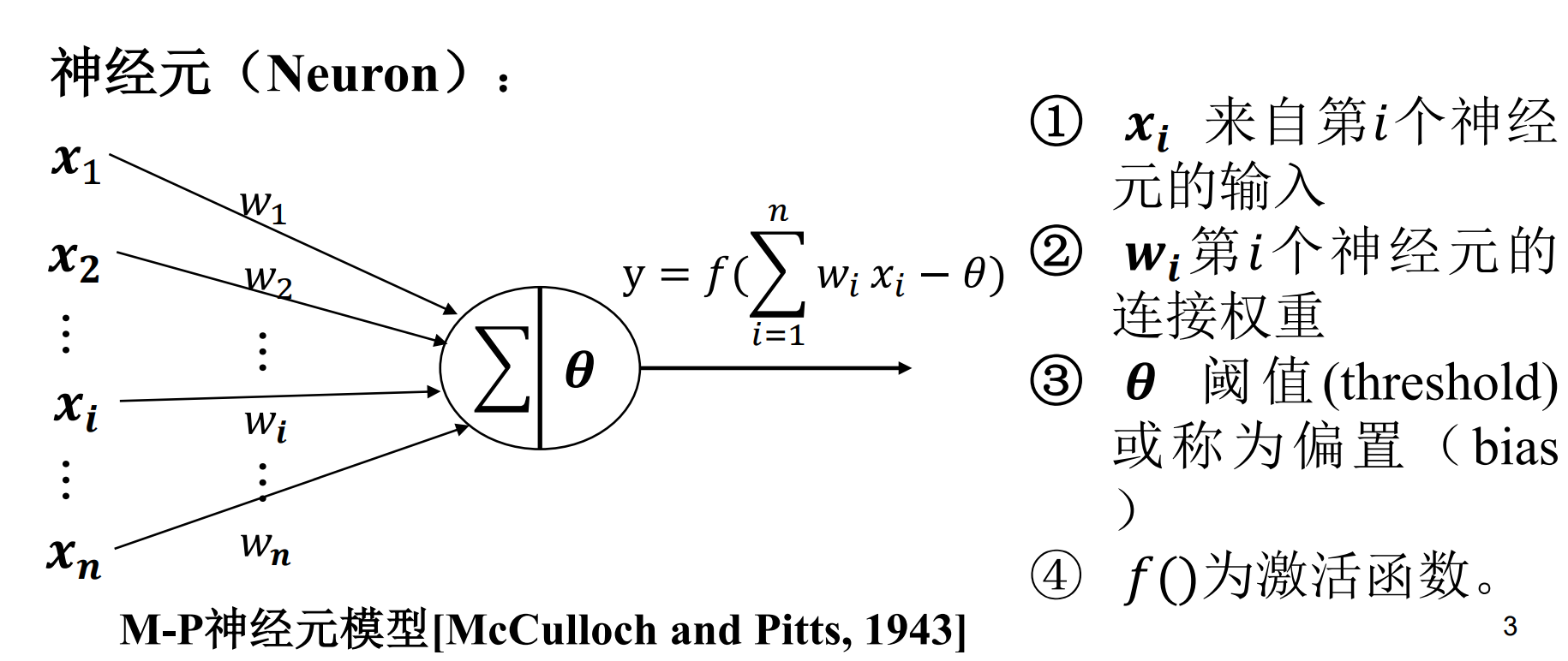
16869849328281686984932728.png

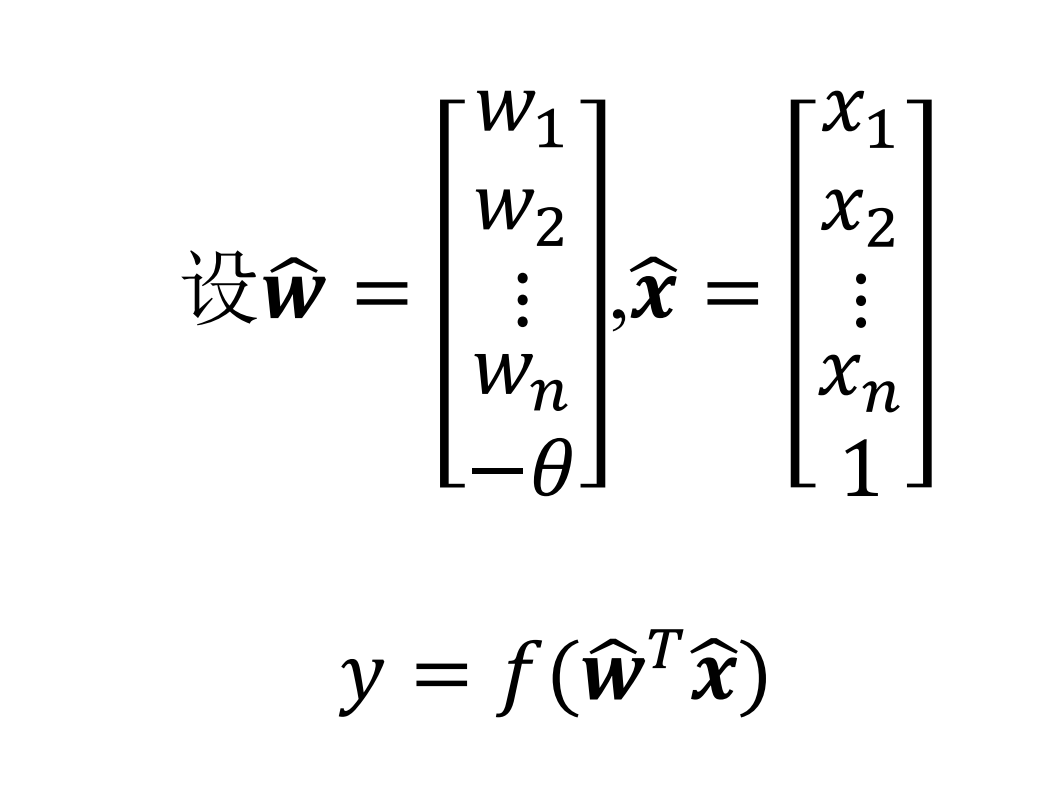
16869850019231686985001125.png

sigmoid function不是某一个函数，而是指某一类形如"S"的函数，都可以成为sigmoid的函数.

支持向量机(SVM)

如果一个数据集是线性可分的，那么一定存在无数 多个超平面将两个类别完全分开。

主观上说，离分类边界远的样本的置信度高， 而离分类边界近的样本的置信度低。

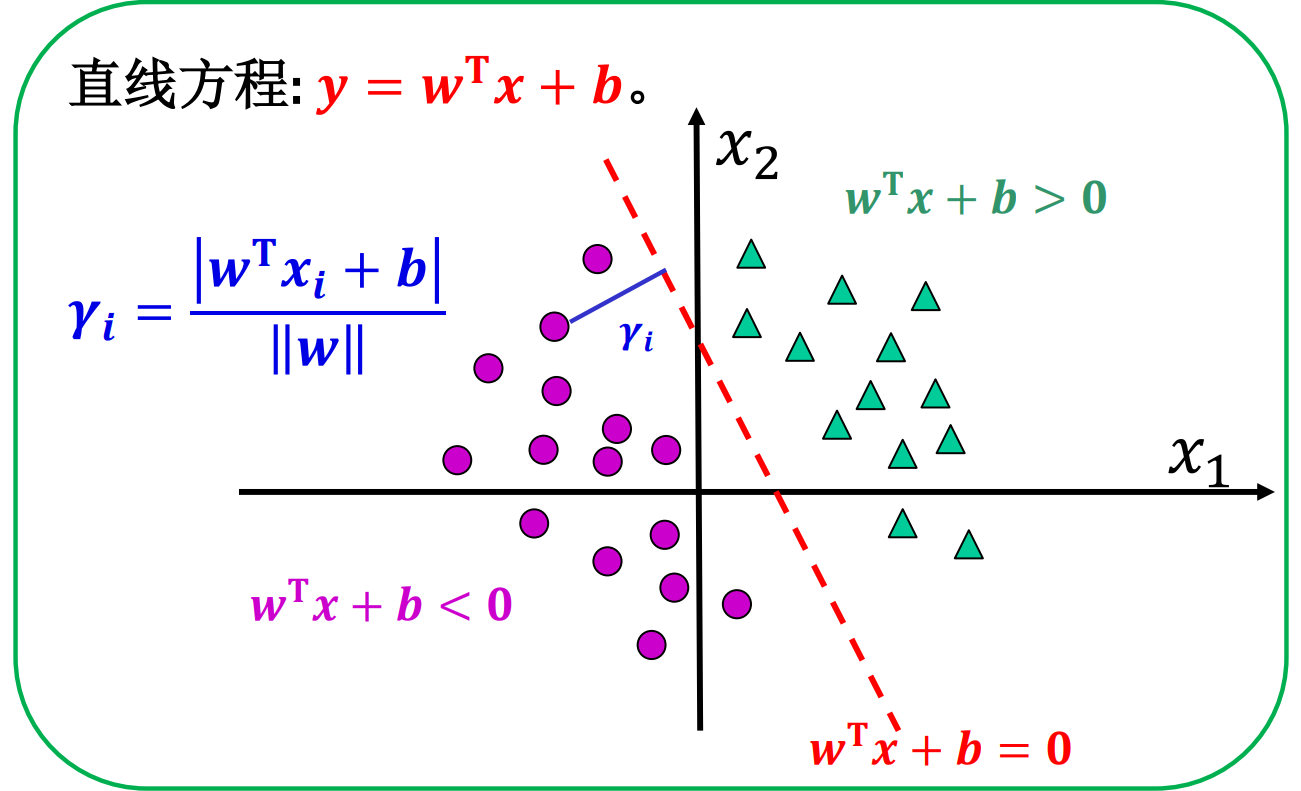
16869855529271686985552022.png

16869856969281686985695852.png

16869901529191686990151887.png

逻辑回归算法是基于全部样本的二分类器：考虑 全部样本的平均似然性。

支持向量机算法是基于部分样本的二分类器：考 虑部分靠近边界的支持向量。

16869906239231686990622967.png

  • 支持向量机的基本思想是寻找两类样本之间最中间的超平面。
  • 支持向量机的目的是使划分平面对于样本的扰动容忍性好。
  • 逻辑回归算法是基于全部样本的二分类器：考虑 全部样本的平均似然性。
  • 支持向量机算法是基于部分样本的二分类器：考 虑部分靠近边界的支持向量。

16869907588371686990758443.png

16869908998291686990899587.png

16869910088311686991008618.png

16869910229161686991021903.png

聚类

聚类：根据某种相似性，把一组数据划分成若干个簇的过程。

难点：

  • 相似性很难精准定义
    • 各种距离，度量学习。
  • 可能存在的划分太多
    • 避免穷举，优化算法
  • 多少个簇
    • 预先给定，算法自适应。

聚类问题可以通过为每个簇 寻找合适的中心来实现。

假设每个簇的中心已经找到， 可以把所有数据点分配到距 离它最近的中心所在的簇。

16869971778691686997177795.png

16869972158921686997214938.png

16869973148871686997314151.png

求解非凸组合优化问题的两种常见方法：

• 启发式方法 (Heuristic method) ：一个基于直观或经验构造的算法，在可接受的时间内下给出待解决组合优化问题每一个实例的一个 可行解，该可行解与最优解的偏离程度一般 不能被预计。

• 松弛方法 (Relaxation method) ：对组合优化问题进行适当的松弛，将其转化为多项式时间内可解的优化问题，松弛后问题的解不是原组合优化问题的解，需要适当的后处理。

16869974168961686997415855.png

优势：

• Lloyd 算法属于EM算法（期望最大化），可以保证收敛到K-means问题的局部最优解。

• Lloyd 算法的速度快，计算复杂度为O(nk)。

• Lloyd 算法思想简单，容易实现，可拓展性强。

劣势：

• 簇的个数 k 需要预先给定。

• 聚类结果依赖于初值的选取。

K-means++是一种初始化方法，目的是改进K-means算 法对初值的影响。

Step 1：随机选取一个簇的中心 𝝁𝟏

Step 2: 选择离已有中心最远的数据点作为新的中心

Step 3: 重复Step 2直到选出 𝑘个中心

Step 4: 运行K-means算法

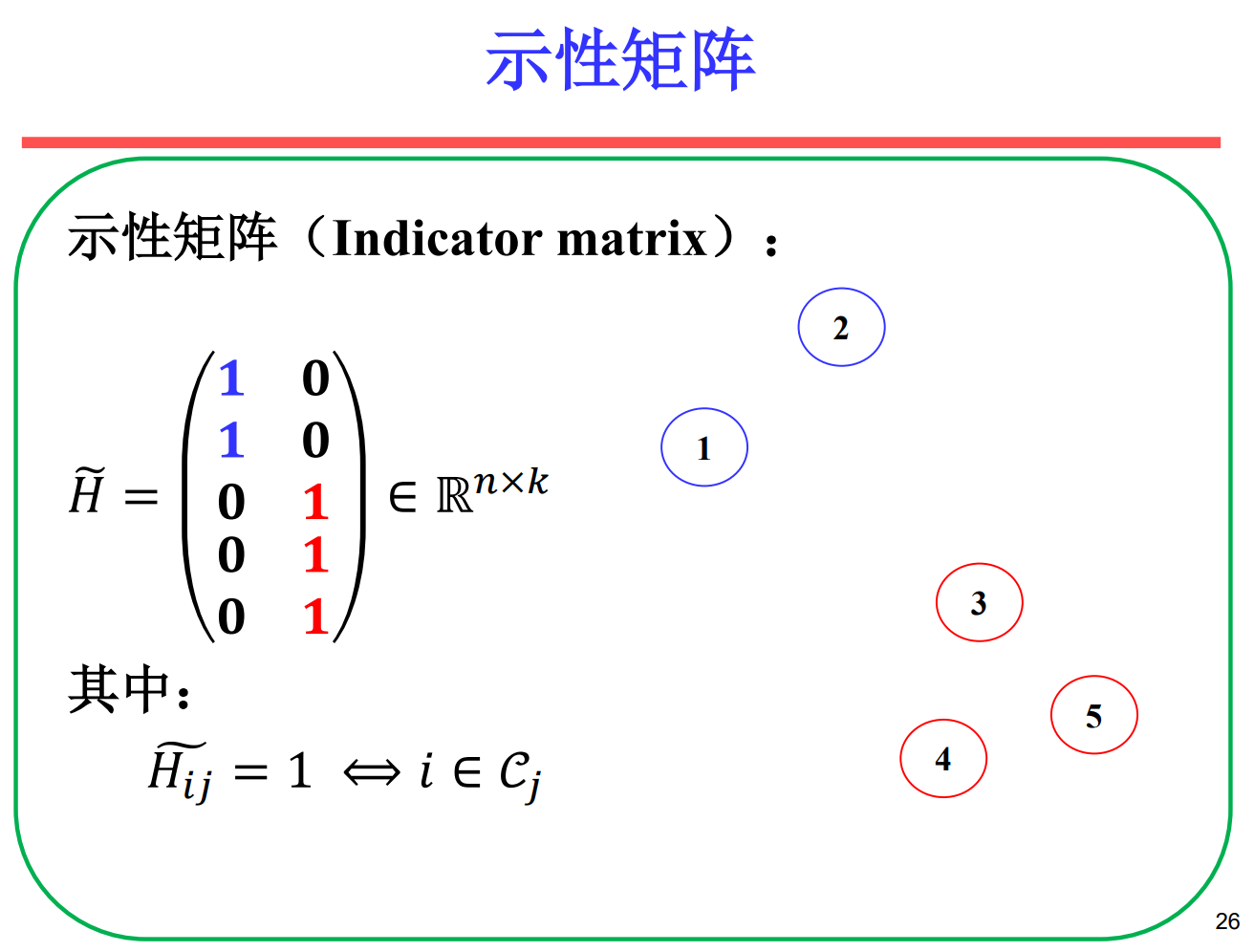
16869976728011686997672682.png

16869977598081686997759603.png

所有标准化示性矩阵都满足

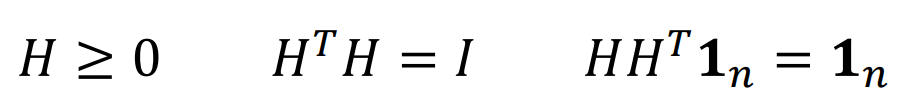
16869980287971686998028721.png

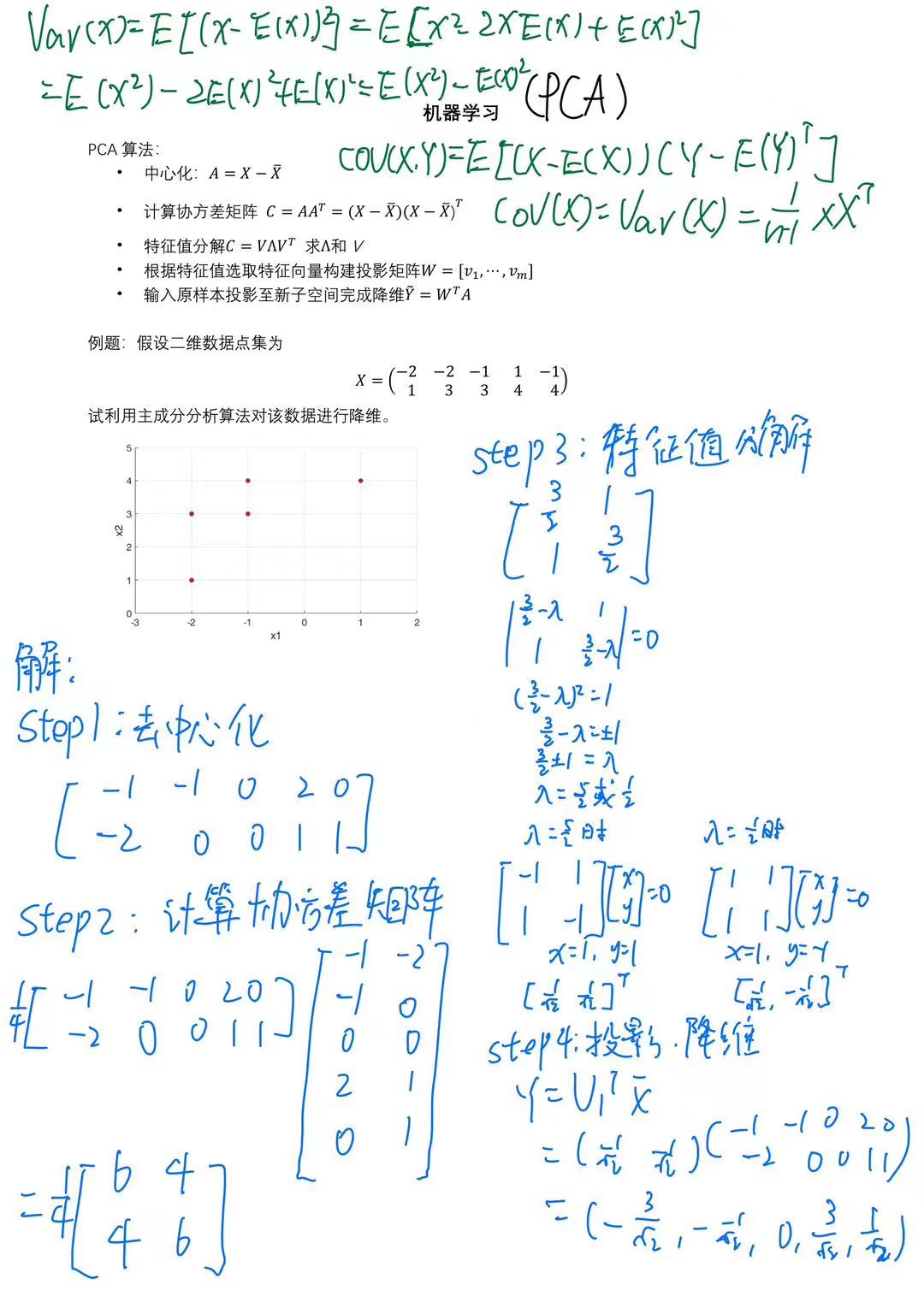
主成分分析

最大方差理论（信号处理领域，Signal Processing）

在信号处理中认为信号具有较大的方差，噪声有较小的方 差。

核心思想：通过正交变换将一组可能存在相 关性的变量转换为一组线性不相关的变量， 达到数据压缩的目的。 即，寻找合适的正交投影矩阵 W，使得投影 之后的样本 𝒀=𝑾𝐓𝑿𝒀 = 𝑾^𝐓𝑿 方差达到最大。

主成分分析(Principal Component Analysis, PCA)目标函数——新坐标系最大化数据新表征的方差:

max⁡wvar(y):=∑i=1n(yi−yˉ)2,s.t.yi=wTxi,∣∣w∣∣=1\max\limits_{w}var(y):=\sum\limits_{i=1}^n(y_i-\bar{y})^2,\text{s.t.}y_i=w^Tx_i,||\text{w}||=1

max⁡Tr(Var(Y))s.t.Y=WTX,WTW=I\begin{gathered} \max\textbf{Tr}(\textbf{Var}(Y)) \\ \text{s.t.}Y=W^{\text{T}}X,W^{\text{T}}W=I \end{gathered}

假设 𝒀=𝑾𝐓𝑿𝒀 = 𝑾^𝐓𝑿是经过变换之后的数据

16869988768971686998875912.png

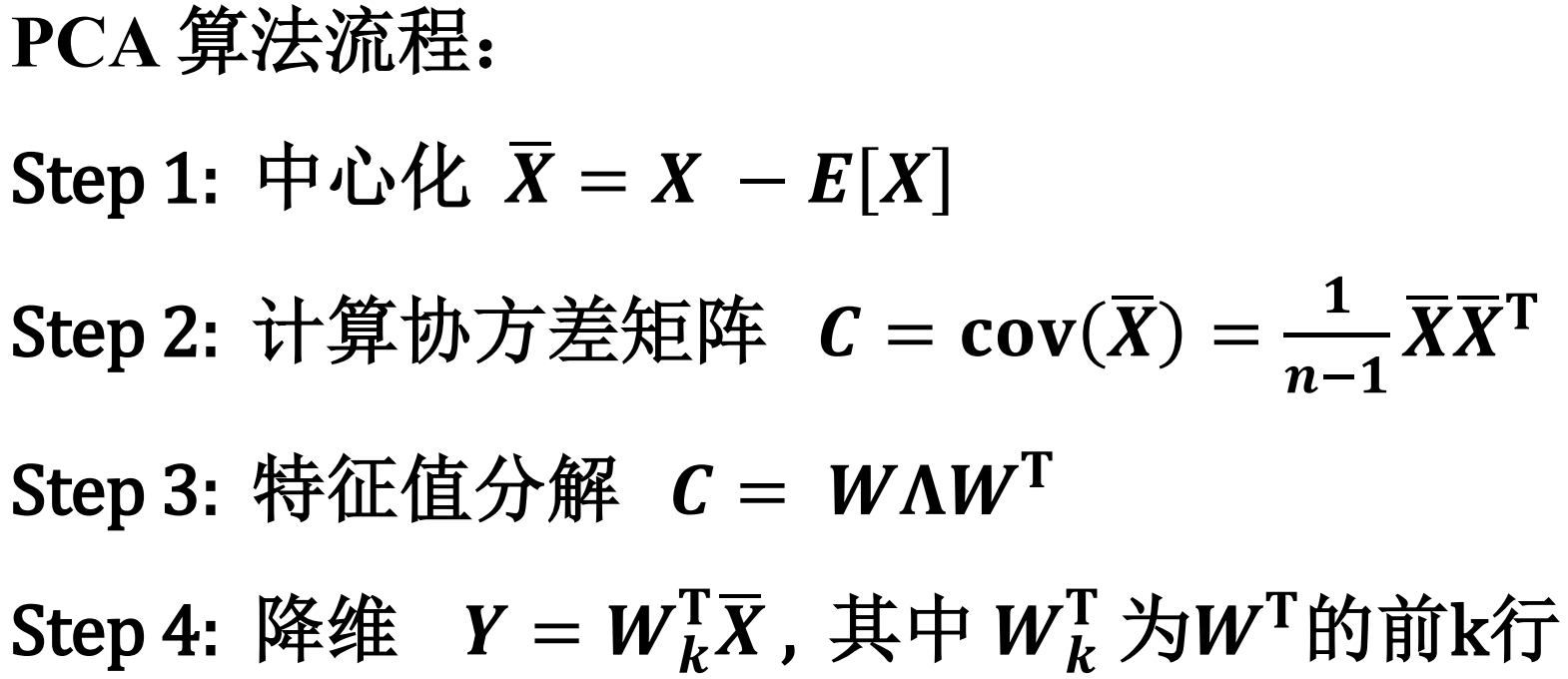
16869989677961686998966856.png

PCA的缺点

  1. 在数据完全未知的情况下，PCA变换不能得到较好的保留数据信息
  2. 对降维得到到最终数据数目不能很好地估计
  3. 假设相关性是线性的，对于非线性的依赖关系不能得到较好的结果
  4. 假设变量服从高斯分布

对协方差矩阵求出来的特征向量，就是新坐标轴方向、数据的旋转方向或者说是新的主成分方向。

对协方差矩阵求出来的特征值，就是数据在对应新坐标轴上投影的方差大小，或者说是其对应特征向量上包含的信息量。

PCA在考虑数据降维时候希望在新空间的信息越多越好，即低维嵌入(embedding)的方差(协方差矩阵的迹)越大。

• PCA是一个无监督降维方法（Unsupervised DR） ， 并没有运用任何有监督信息 （ Supervised Information），这也是PCA算法一个弊端。

• 对于一个分类问题，保留信息越多分类效果一定 会更好么？ – 不一定，分类效果完全取决样本在新的子空间下的可区分度。

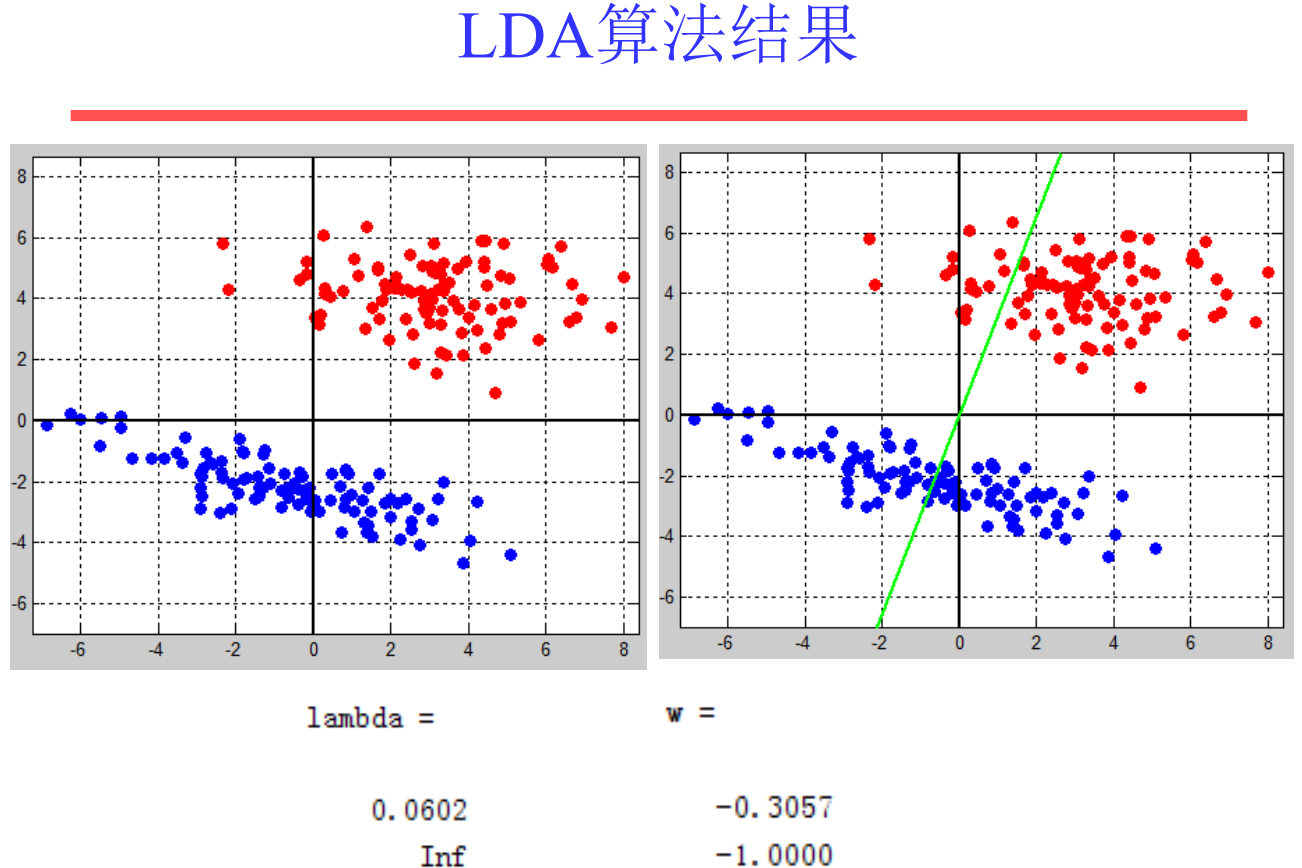
LDA

降维+分类

假设降维的目的是解决维度灾难，在低维空间进行分类。那么我们希望降维后的样本保持一定的可分性，即经过投影之后，同类样本的投影点尽可能接近，异类样本的投影点尽可能远离 。

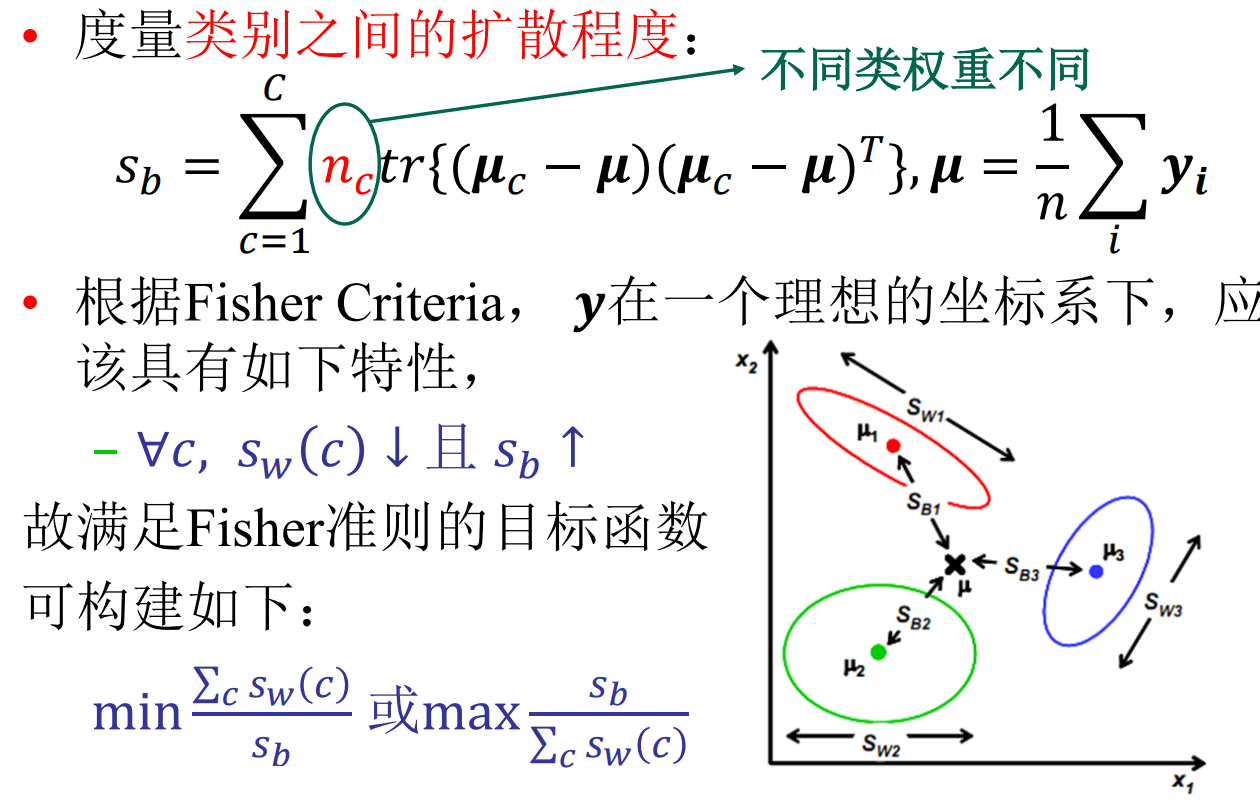
让投影后的类中心之间的距离尽可能大，从而增强样本的可分性。

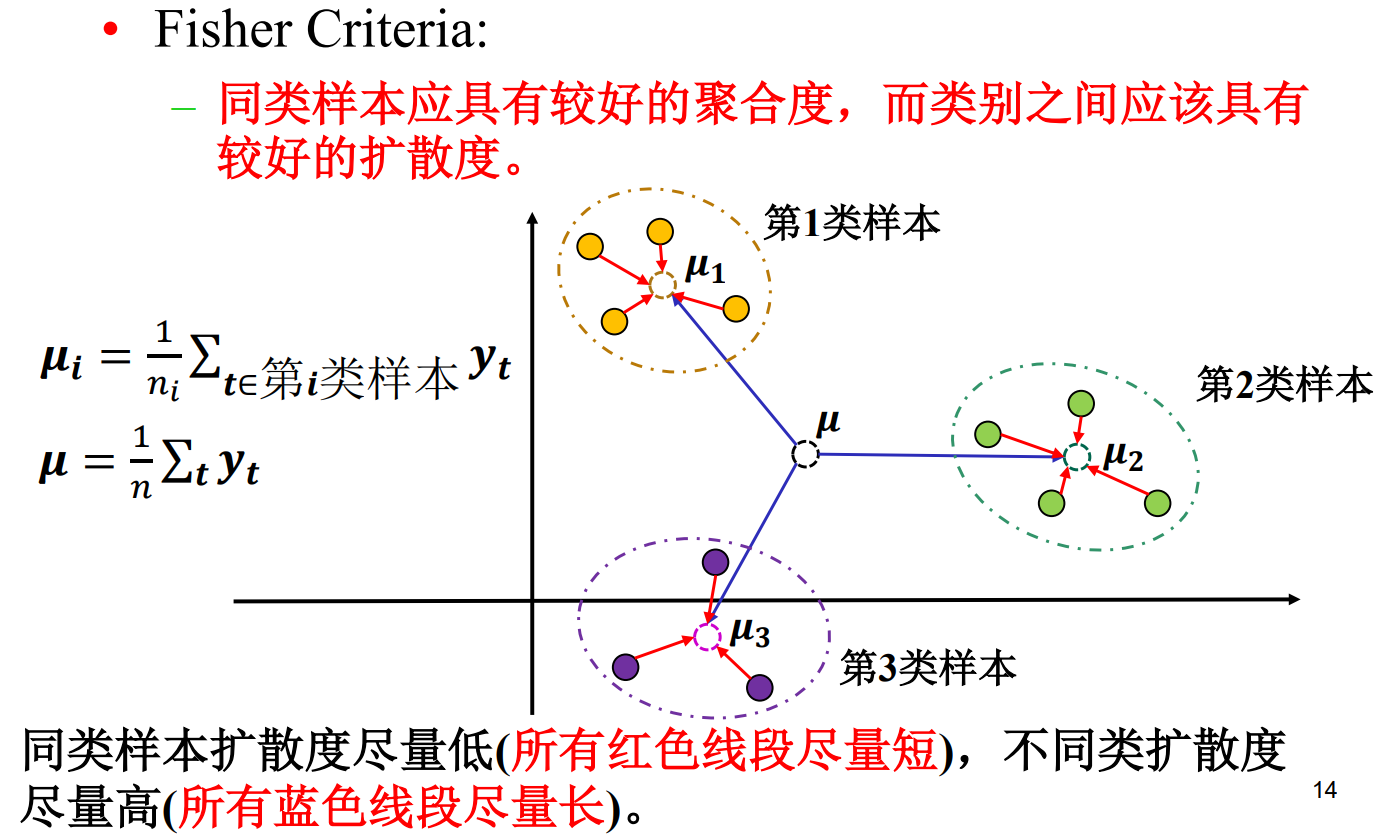
同类样本应该尽量聚合在一起，而不同类样本之间 应该尽量扩散。

由于线性判别分析用到fisher criteria,所以又称费舍儿判别 分析(Fisher Discriminant Analysis, FDA)!

16870057087681687005707906.png

16870059797771687005979553.png

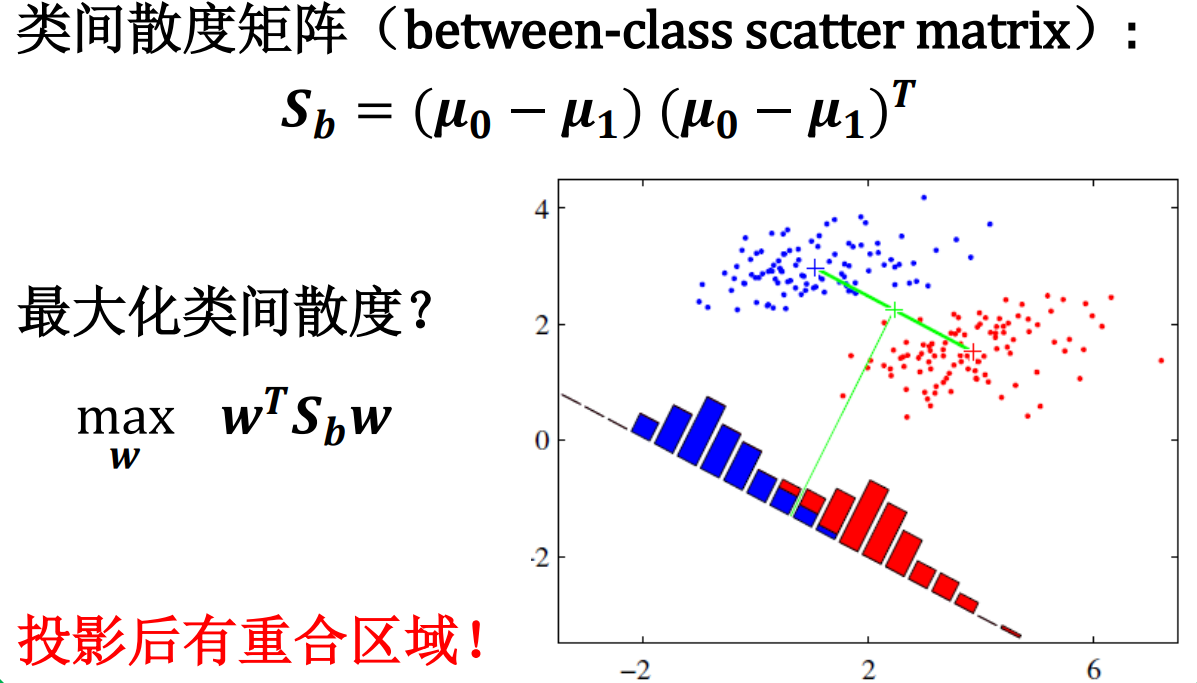
16870059977651687005997501.png

16870060967711687006096058.png

16870062068541687006205911.png

image-20230617205253688

16870064577791687006457371.png

16870064828561687006482128.png

𝑆𝑆 𝑏𝑏不满秩，没有矩阵逆，LDA求解不稳定。

解决方案？ – 正则化 – 先PCA后LDA

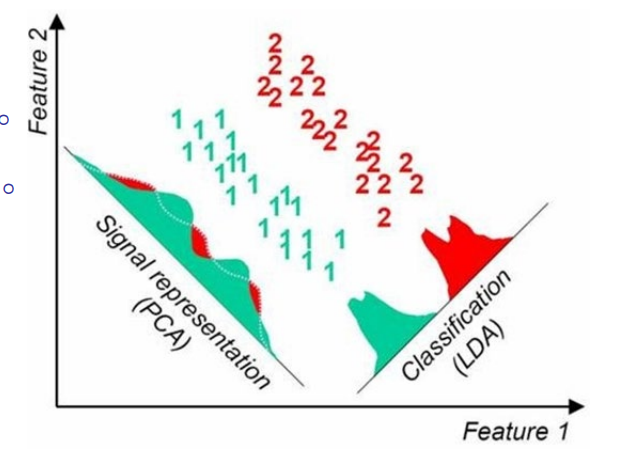
PCA与LDA对比

– PCA旨在寻找一组子坐标系（定义一个子空间）使得样本点的方差最大，即信息量保留越多。

– LDA旨在寻找一组子坐标系（定义一个子空间）使得样本点类内散度越小，类间散度越大（Fisher Criteria）。

监督性： – PCA是无监督学习方法。 – LDA是有监督学习方法。

算法效率 – PCA效率更胜一筹

16870066317781687006631395.png

16870073447661687007344414.png

16871370790406d7173fd046b5c9d3ea225f9f4d29e9.jpg

168713708304514b87252bf5d772af7ade1ca364ddd2.jpg

168713708914113dd664641a6f930b21d4a7c0574477.jpg

1687137096041071eaa406893bf17fa7f4ccbe44f7c2.jpg

1687137100051ab164407747298d73a6cf7d9031df18.jpg

16871371050409a74c940d1e80cbf6ef6516c6e04580.jpg

1687137110039fe74bce91ccb3df521baf5d2f76d097.jpg