Overcoming catastrophic forgetting in neural networks（EWC）

摘要

Our approach remembers old tasks by selectively slowing down learning on the weights important for those tasks.

通过有选择地减缓对那些任务重要的权重的学习来记忆旧任务。

该算法根据它们对先前看到的任务的重要性来减缓对某些权重的学习。

EWC

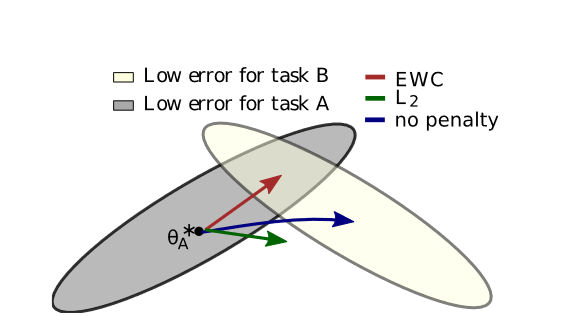
弹性权重整合( EWC )确保在对任务B进行训练的同时记住任务A。

训练轨迹在示意性参数空间中显示，参数区域在任务A (灰色)和任务B (黄色)上表现良好。

在学习完第一个任务后，参数在θA*处。如果我们单独根据任务B采取梯度步骤(蓝色箭头)，我们将最小化任务B的损失

但破坏了我们对任务A的学习。另一方面，如果我们用相同的系数(绿色箭头)约束每个权重，施加的限制过于严厉，我们只能记住任务A，而不学习任务B。

EWC，相反，通过显式计算任务A的重要权重，找到任务B的解决方案，而不会对任务A造成显著的损失(红色箭头)

we approximate the posterior as a Gaussian distribution with mean given by the parameters θ∗ A and a diagonal precision given by the diagonal of the Fisher information matrix F .

F有三个关键性质：

( a )它等价于损失在极小值附近的二阶导数

( b )它可以从一阶导数单独计算，因此即使对于大模型也很容易计算

( c )它保证是半正定的。注意，这种方法类似于期望传播，其中每个子任务被视为后验的一个因子。给定这个近似，我们在EWC中最小化的函数L为：

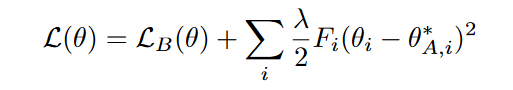
When moving to a third task, task C, EWC will try to keep the network parameters close to the learned parameters of both task A and B. This can be enforced either with two separate penalties, or as one by noting that the sum of two quadratic penalties is itself a quadratic penalty.当移动到第三个任务时，任务C，EWC会尽量使网络参数接近任务A和B的学习参数。这可以通过两个单独的惩罚来实现，也可以通过注意两个二次惩罚的总和本身就是一个二次惩罚来实现。

结论

在任务差异不大情况下，EWC确实是一个有效的方法，理论也很优雅，但任务差异较大时，泰勒展开的高阶项就不能近似为0，导致了EWC方法不好的表现，此外，参数之间是有关联分布的(假设应该他们是混合高斯)，EWC取费雪信息矩阵的对掉线忽略了参数相关性，这些都是EWC的不足

相关的数学知识

正定：

e.g.

半正定

直观解释

EWC 方法中使用 Fisher 信息矩阵来量化先前任务对当前任务的影响，并根据这些影响来进行正则化。

具体来说，Fisher 信息矩阵可以用于计算每个先前任务所对应的权重矩阵在当前任务中的重要性。在 EWC 方法中，这些重要性被用来计算每个先前任务的正则化系数，以保护这些先前任务的权重矩阵不被过度调整。

具体来说，假设我们已经完成了 KK 个任务的连续学习过程，每个任务都有一个对应的权重矩阵 θk\theta_k。在学习第 K+1K+1 个任务时，我们希望保留前面 KK 个任务的知识，同时又能够在当前任务上学习到新的知识。

为了保留前面 KK 个任务的知识，我们需要对它们的权重矩阵进行正则化。对于第 kk 个任务的权重矩阵 θk\theta_k，我们可以使用 Fisher 信息矩阵 FkF_k 来计算它在当前任务中的重要性。具体来说，我们可以计算第 kk 个任务的正则化系数为：

λk=Fkα+Fk\lambda_k = \frac{F_k}{\alpha + F_k}

其中，α\alpha 是一个超参数，用于调整正则化的强度。这个正则化系数表示了第 kk 个任务对当前任务的重要性，重要性越高，正则化系数越大。

然后，我们可以使用这些正则化系数来更新当前任务的损失函数。具体来说，我们可以将当前任务的损失函数表示为：

J(θ)=JK+1(θ)+∑k=1KλkJk(θ)J(\theta) = J_{K+1}(\theta) + \sum_{k=1}^K \lambda_k J_k(\theta)

其中，JK+1(θ)J_{K+1}(\theta) 是当前任务的损失函数，Jk(θ)J_k(\theta) 是第 kk 个任务的损失函数，λk\lambda_k 是第 kk 个任务的正则化系数。这个损失函数包括了当前任务的损失函数和前面 KK 个任务的正则化项，以保护前面任务的权重矩阵不被过度调整。

通过这种方式，EWC 方法可以保留前面任务的知识，同时又能够在当前任务上学习到新的知识。而 Fisher 信息矩阵则在计算正则化系数时起到了关键作用，它能够量化先前任务对当前任务的影响，并根据这些影响来进行正则化。

正则化系数是一种用于控制正则化强度的系数，通常用于保护模型不被过度拟合。在 EWC 方法中，正则化系数用于保护之前学习的任务，以避免新任务学习到的知识对之前学习的任务造成过大的影响。

具体来说，在 EWC 方法中，每个先前任务的正则化系数可以由 Fisher 信息矩阵计算得到。Fisher 信息矩阵可以衡量模型参数的灵敏度，即模型参数的变化对损失函数的影响程度。对于第 kk 个先前任务，它的 Fisher 信息矩阵可以表示为：

Fk=EDk[(∂log⁡p(Dk∣θ)∂θ)2]F_k = \mathbb{E}_{\mathcal{D}_k}\left[\left(\frac{\partial \log p(\mathcal{D}_k|\theta)}{\partial \theta}\right)^2\right]

其中，Dk\mathcal{D}_k 是第 kk 个任务的数据集，p(Dk∣θ)p(\mathcal{D}_k|\theta) 是模型在第 kk 个任务上的概率分布，θ\theta 是模型的参数。这个 Fisher 信息矩阵可以用来衡量第 kk 个任务对当前任务的影响，从而计算出第 kk 个任务的正则化系数。

具体来说，第 kk 个任务的正则化系数可以表示为：

λk=Fkα+Fk\lambda_k = \frac{F_k}{\alpha + F_k}

其中，α\alpha 是一个超参数，用于调整正则化的强度。这个正则化系数表示了第 kk 个任务对当前任务的重要性，重要性越高，正则化系数越大。在 EWC 方法中，这个正则化系数用于保护之前学习的任务，以避免新任务学习到的知识对之前学习的任务造成过大的影响。

总之，正则化系数是一种用于控制正则化强度的系数，它可以通过 Fisher 信息矩阵计算得到。在 EWC 方法中，正则化系数用于保护之前学习的任务，以避免新任务学习到的知识对之前学习的任务造成过大的影响。

当我们使用 EWC 方法进行多任务学习时，假设我们已经学习了两个任务，任务1和任务2，并且我们想要在这两个任务的基础上学习一个新的任务3。在这种情况下，我们需要使用 EWC 方法来保护任务1和任务2的权重矩阵，避免它们被过度调整，从而保护之前学习的知识。

假设我们的模型有 nn 个参数，那么每个任务的 Fisher 信息矩阵的大小为 n×nn \times n。对于任务1和任务2，我们可以计算它们各自的 Fisher 信息矩阵 F1F_1 和 F2F_2，然后计算它们各自的正则化系数 λ1\lambda_1 和 λ2\lambda_2。这个计算方式可以使用以下公式：

λk=Fkα+Fk\lambda_k = \frac{F_k}{\alpha + F_k}

其中，kk 表示任务的编号，α\alpha 是一个超参数，用于调整正则化的强度。

假设我们得到了任务1和任务2的正则化系数 λ1\lambda_1 和 λ2\lambda_2，然后我们想要在任务1和任务2的基础上学习一个新的任务3。在学习任务3的过程中，我们需要对任务1和任务2的权重矩阵进行保护，以避免它们被过度调整。

具体来说，我们可以使用以下的损失函数来学习任务3：

L=L3+∑k=12λk2∣∣θ−θk∣∣2L = L_3 + \sum_{k=1}^2 \frac{\lambda_k}{2} ||\theta-\theta_k||^2

其中，L3L_3 是任务3的损失函数，θ\theta 是当前任务的权重矩阵，θk\theta_k 是任务 kk 的权重矩阵，∣∣θ−θk∣∣2||\theta-\theta_k||^2 表示当前任务的权重矩阵和任务 kk 的权重矩阵之间的欧几里得距离的平方，λk\lambda_k 是任务 kk 的正则化系数。

通过在损失函数中添加正则化项，我们可以保护任务1和任务2的权重矩阵，以避免它们被过度调整。在学习任务3的过程中，我们不仅要考虑任务3的损失函数，还要考虑任务1和任务2的正则化项，以确保保护之前学习的知识。

Fisher 信息矩阵是一个衡量模型参数灵敏度的矩阵，它可以用于计算每个先前任务的正则化系数，以保护这些先前任务的权重矩阵不被过度调整。

（部分回答来自GPT）