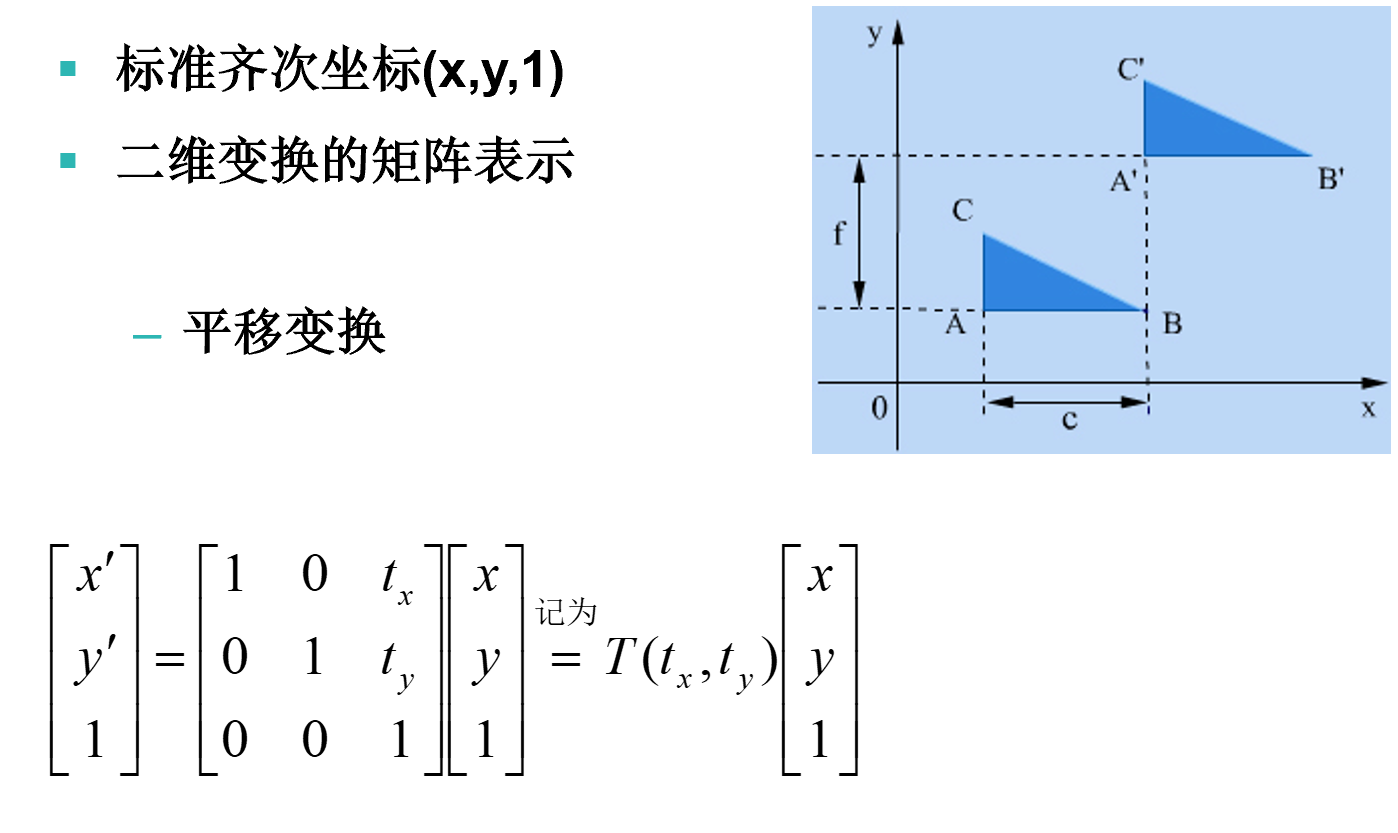
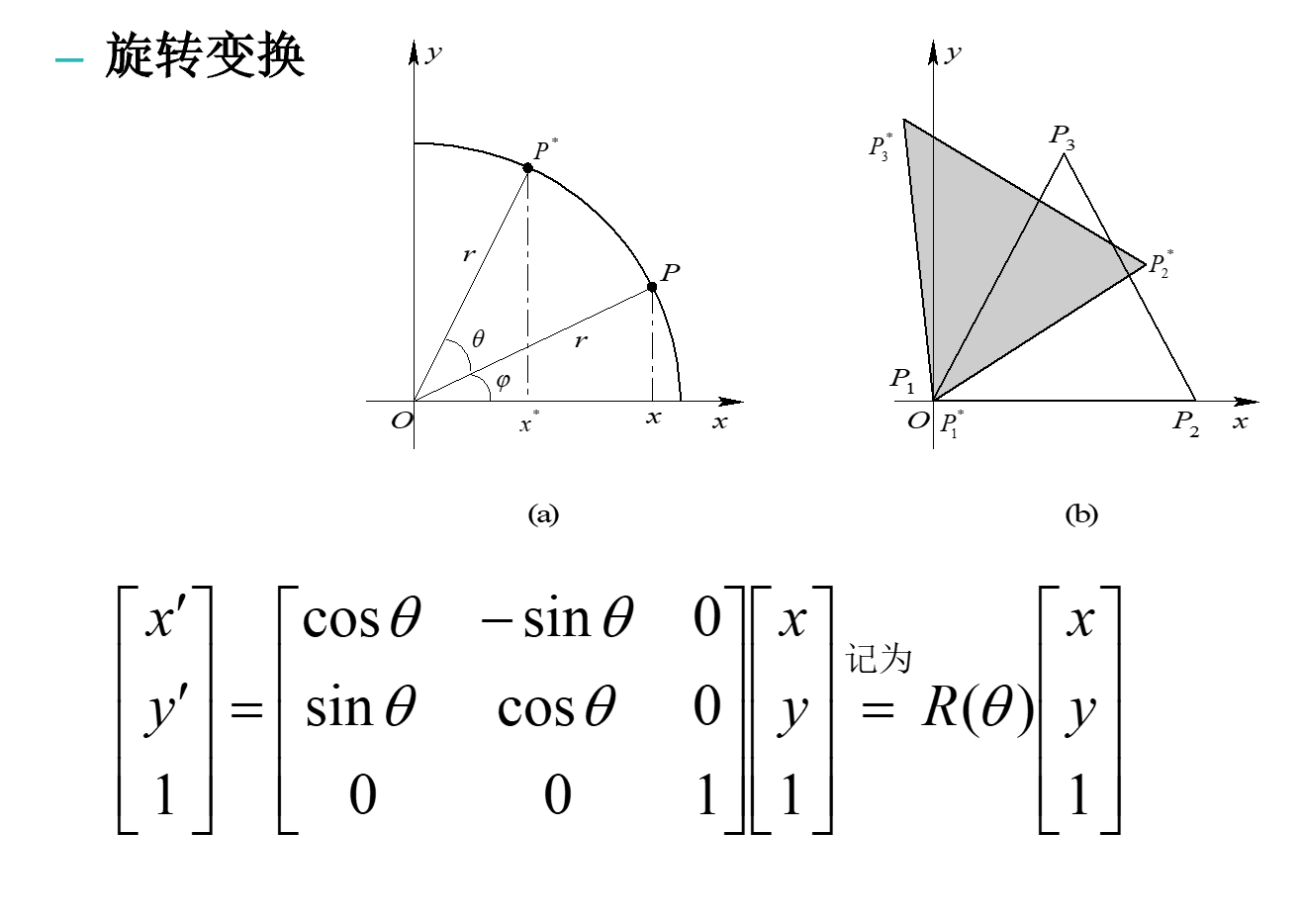
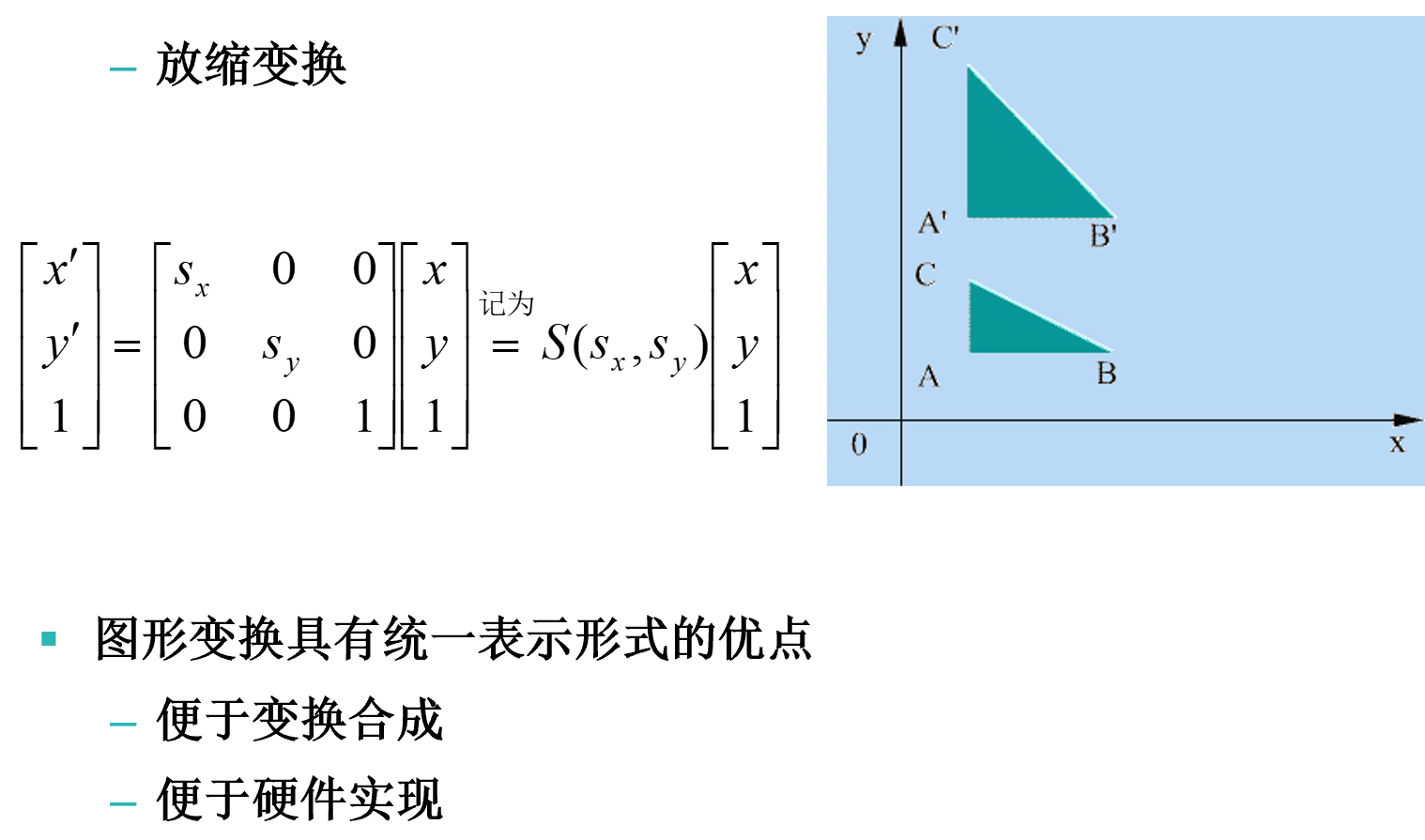
二维图形的变换

§为什么需要齐次坐标？

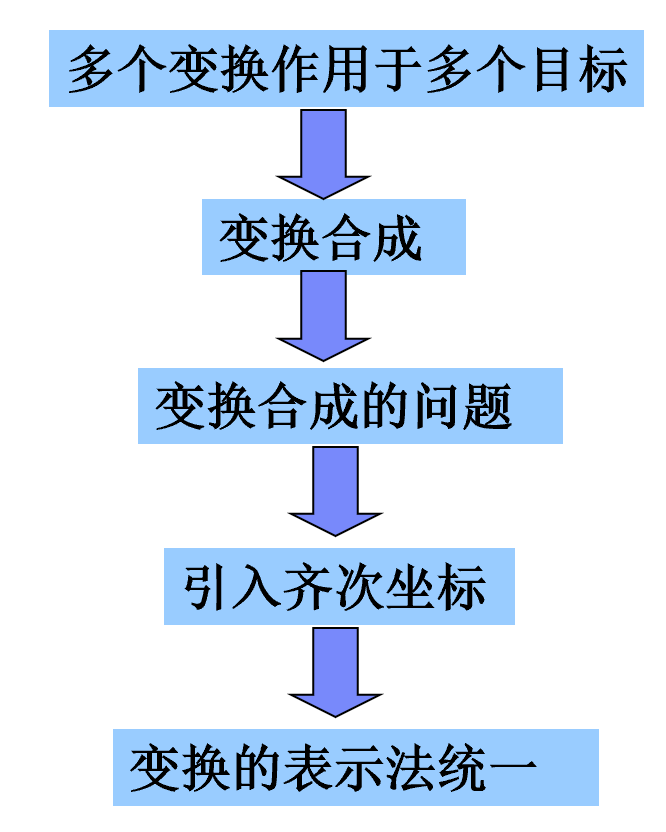
所谓齐次坐标, 就是将一个原本是n维的向量用一个n+1维向量来表示。
例如, 向量(x1, x2, …, xn)的齐次坐标表示为
(Hx1, Hx2, …, Hxn, H), 其中H是一个不为0的实数。

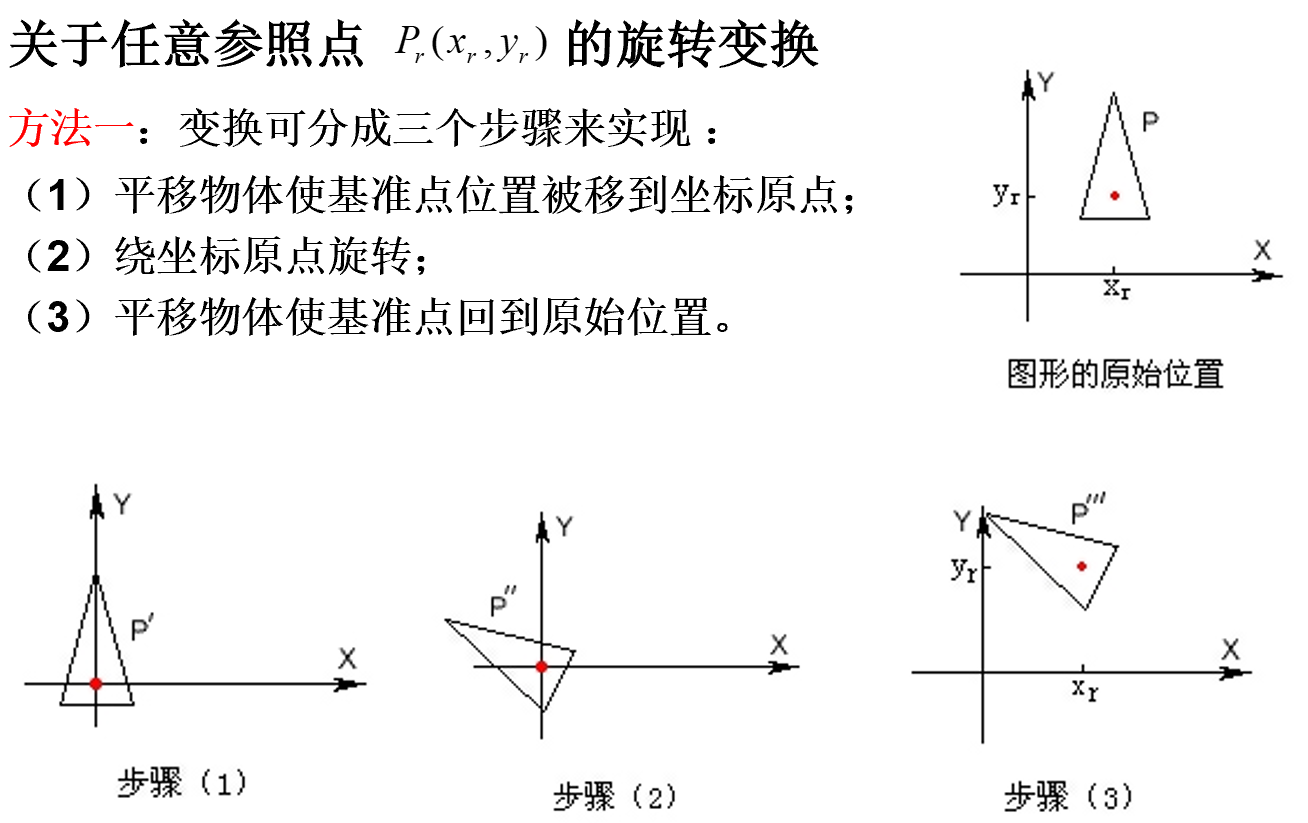
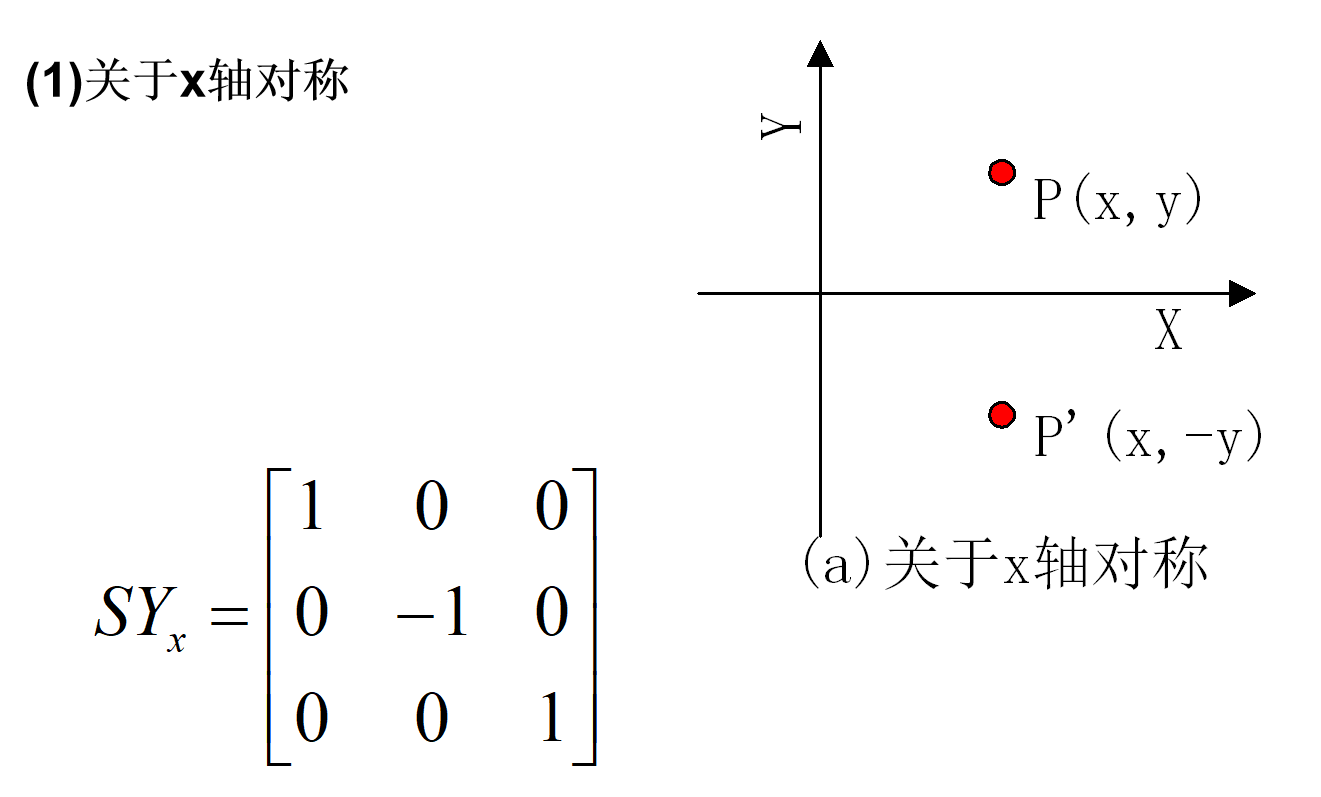
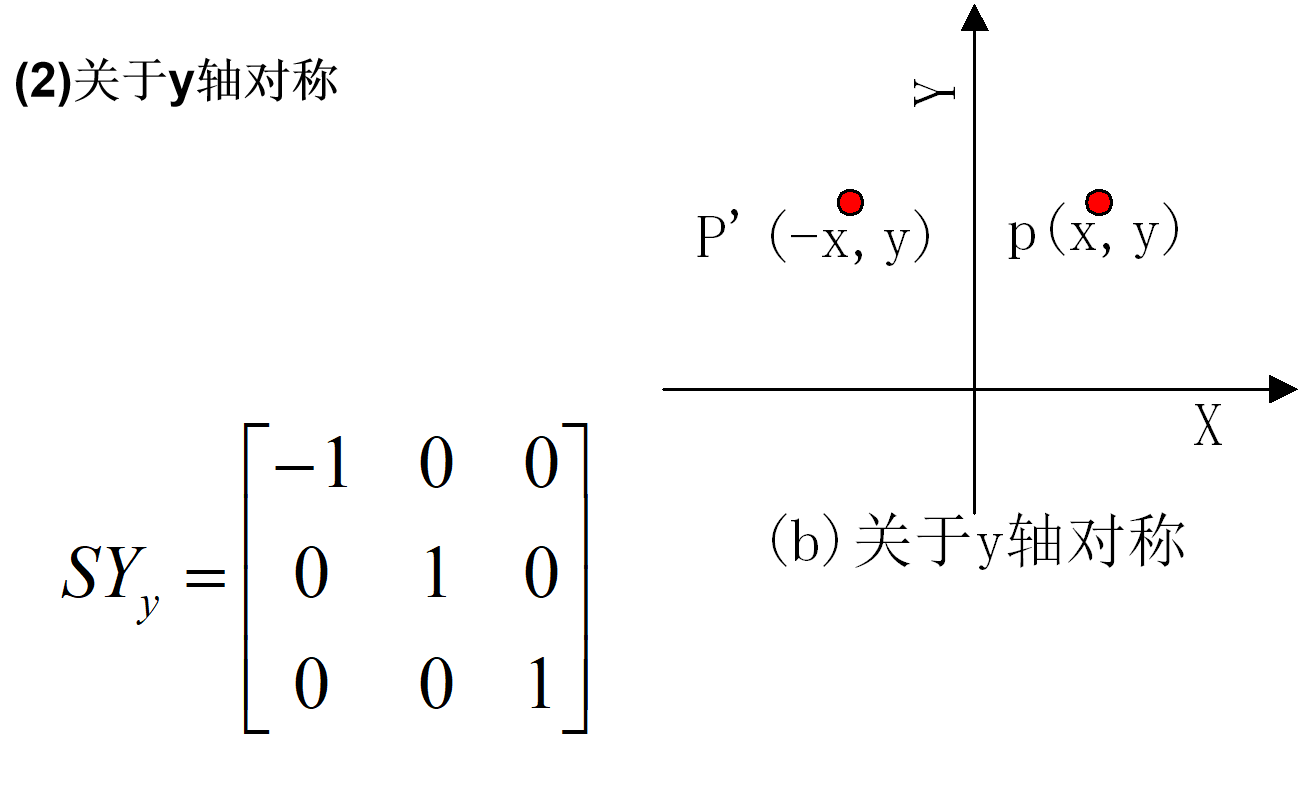
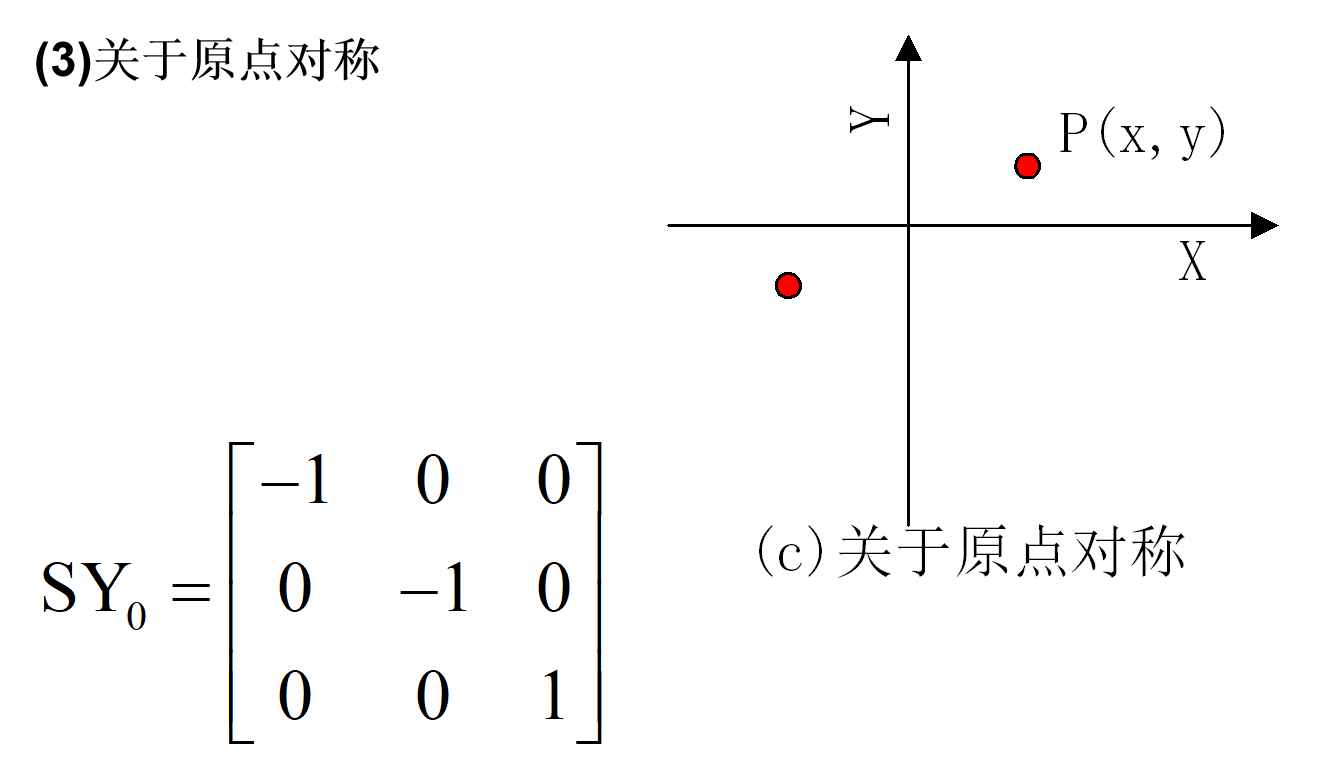
对称变换:变换后的图形是原图形关于某一轴线或原点的镜像。

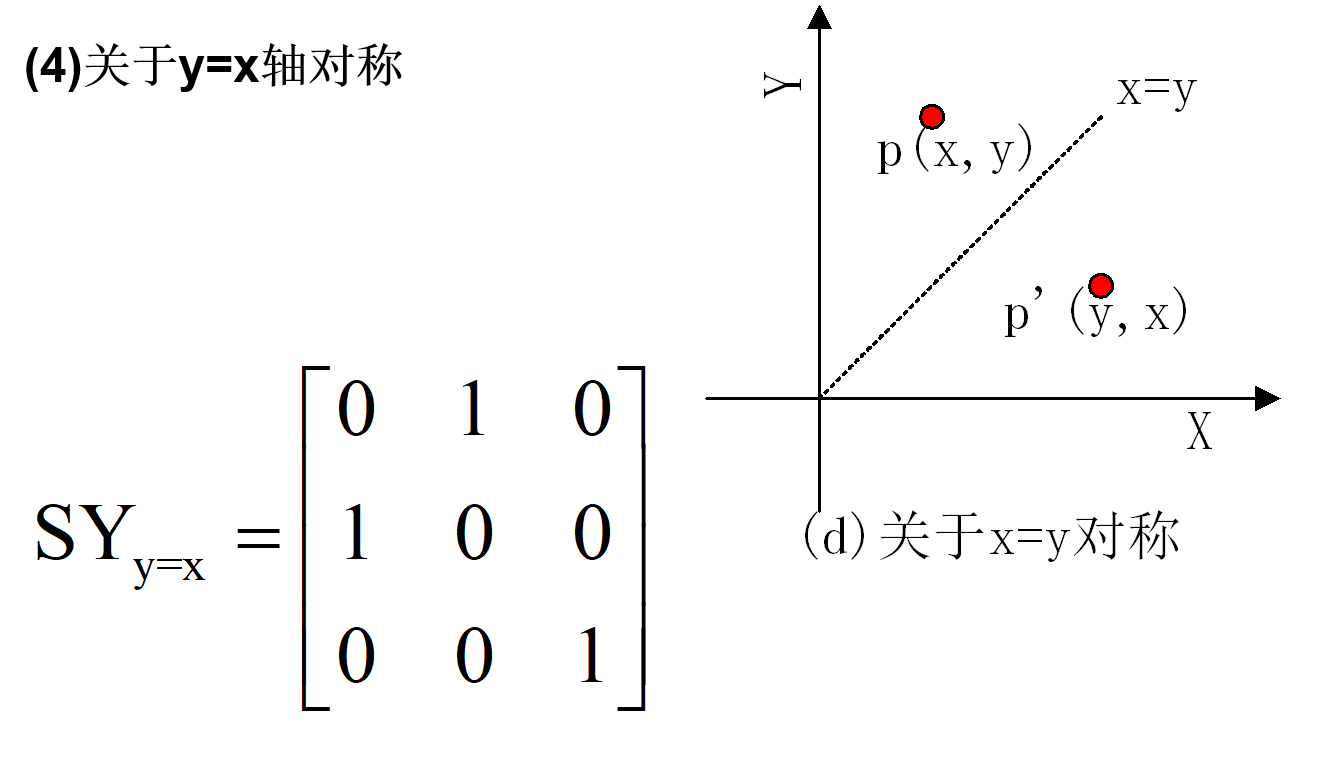
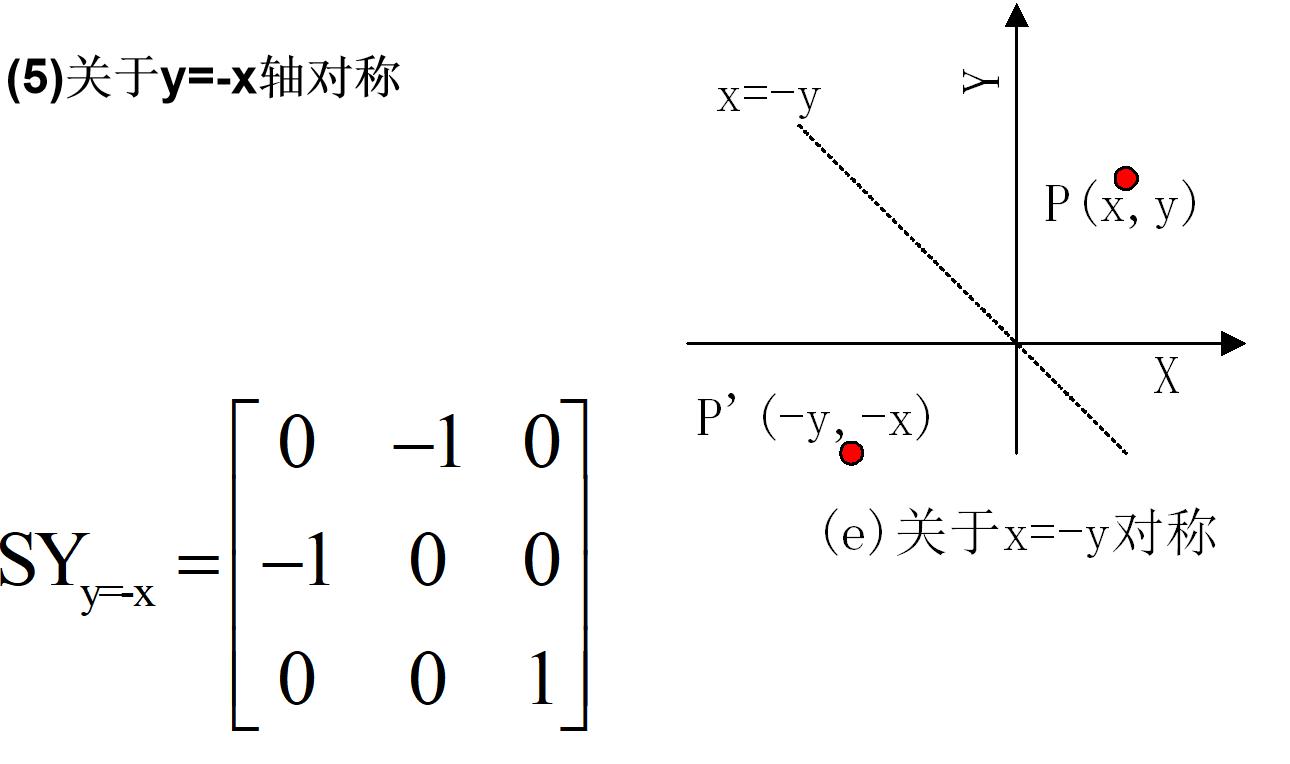
错切变换

也称为剪切、错位变换，用于产生弹性物体的变形处理。

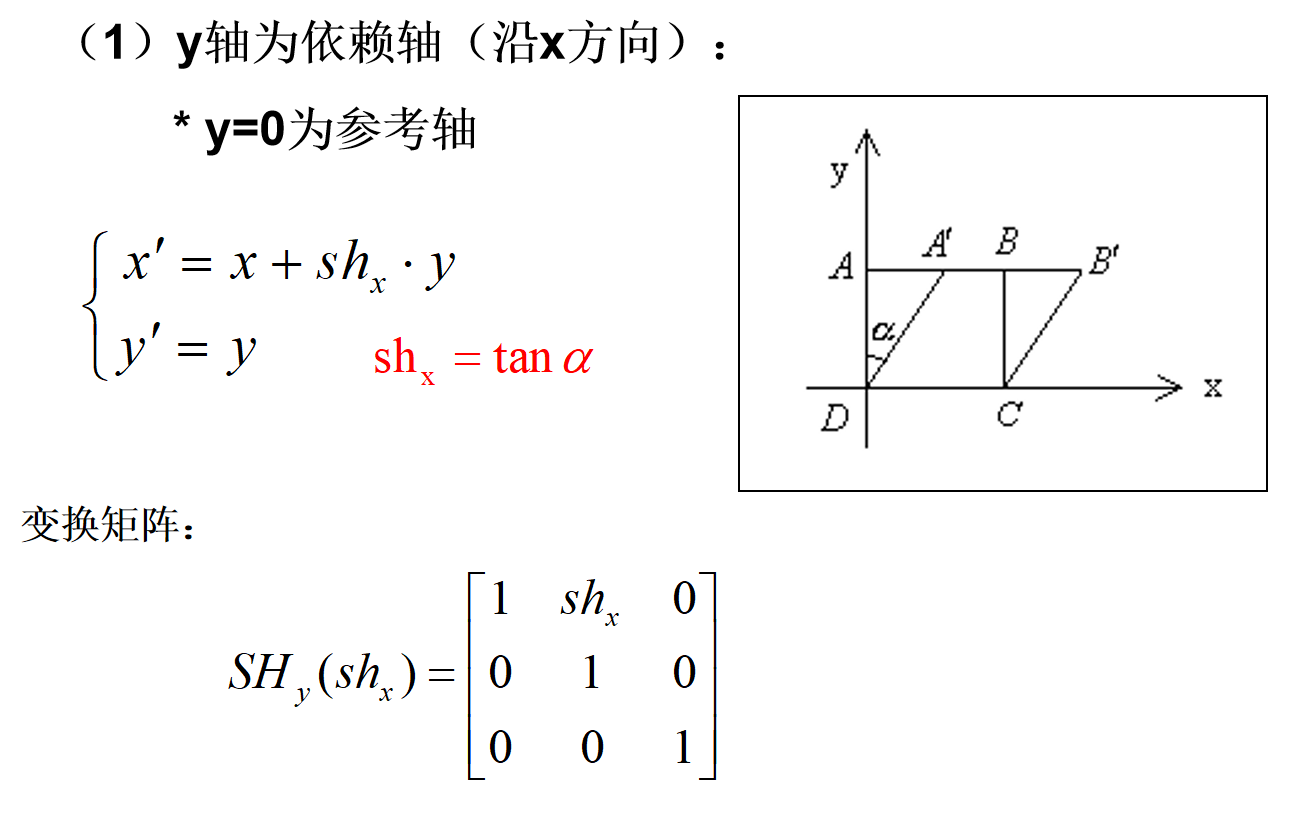
仿射平面（或空间）到自身的一类变换，最重要的性质是保持点的共线性（或共面性）以及保持直线的平行性。

变换的坐标x‘和y’都是原始坐标x和y的线性函数。仿射变换具有平行线转换成平行线和有限点映射到有限点的一般特性。平移、比例、旋转、对称和错切变换是二维仿射变换的特例，任何常用的二维仿射变换总可表示为这五种变换的组合。